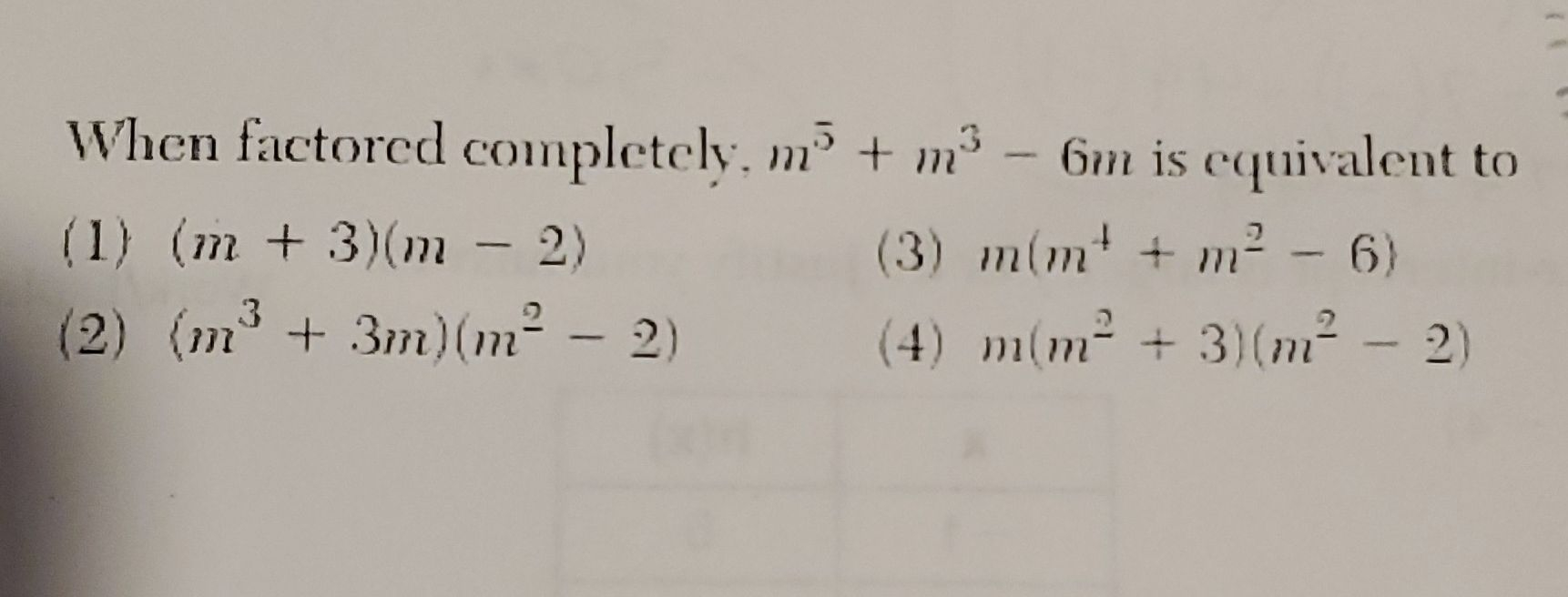When factored completely, m^(5)+m^(3)-6m is equivalent to (1) (m+3)(m-2) (2) (m^(3)+3m)(m^(2)-2) (3) m(m^(4)+m^(2)-6) (4) m(m^(2)+3)(m^(2)-2)

Question

Bytelearn · Accepted Answer

Identify Common Factor: We are given the expression m^(5) + m^(3) - 6m, and we need to factor it completely. The first step is to look for a common factor in all terms.Factor Out 'm': We can see that each term has an 'm' in it, so we can factor out an 'm' from the entire expression. m^(5) + m^(3) - 6m = m(m^(4) + m^(2) - 6)Factor Quadratic-like Expression: Now we need to factor the quadratic-like expression m^(4) + m^(2) - 6. This is similar to factoring a quadratic equation, except that m^(2) is taking the place of a typical 'x' in a quadratic.Find Multiplying Numbers: We look for two numbers that multiply to -6 and add to 1 (the coefficient of m^(2)). These numbers are 3 and -2.Factor Quadratic Expression: We can now factor the expression m^(4) + m^(2) - 6 as (m^(2) + 3)(m^(2) - 2). m(m^(4) + m^(2) - 6) = m(m^(2) + 3)(m^(2) - 2)Final Factored Form: We have factored the expression completely, and the factored form is m(m^(2) + 3)(m^(2) - 2).

When factored completely, $m^{5}+m^{3}-6 m$ is equivalent to $\newline$ ( $1$ ) $(m+3)(m-2)$ $\newline$ ( $2$ ) $\left (m^{3}+3 m\right)\left(m^{2}-2\right)$ $\newline$ ( $3$ ) $m\left(m^{4}+m^{2}-6\right)$ $\newline$ ( $4$ ) $m\left(m^{2}+3\right)\left(m^{2}-2\right)$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics