Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

What is the value of
log_(9)((1)/(9)) ?
Answer:

Evaluate. $\newline$ $\log _{9} \frac{1}{9}$ $\newline$ Write your answer in simplest form.

View step-by-step help

View step-by-step help

Full solution

Q. Evaluate.

\newline

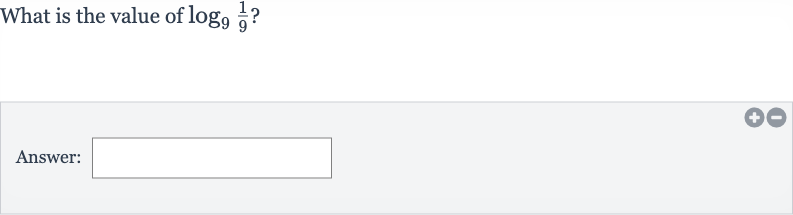
\log _{9} \frac{1}{9}

\newline

Write your answer in simplest form.

Understand the problem: Understand the problem. $\newline$ We need to find the value of the logarithm of $\frac{1}{9}$ with base $9$ . The logarithm $\log_{\text{base}}(b)(a)$ answers the question: ＂To what power must we raise $b$ to obtain $a$ ?＂ In this case, we are looking for the power to which $9$ must be raised to get $\frac{1}{9}$ .
Apply the definition: Apply the definition of a logarithm. $\newline$ We know that $9$ to the power of $-1$ equals $\frac{1}{9}$ (since $\frac{1}{9}$ is the reciprocal of $9$ , and the reciprocal of a number is that number to the power of $-1$ ). Therefore, $\log_{9}\left(\frac{1}{9}\right)$ is asking for the exponent that makes $9$ equal to $\frac{1}{9}$ .
Calculate the logarithm: Calculate the logarithm. $\newline$ Since $9^{-1} = \frac{1}{9}$ , by the definition of logarithms, $\log_{9}\left(\frac{1}{9}\right) = -1$ .

More problems from

Question

One angle of a parallelogram measures

40^\circ

. What are the measures of the other three angles in the parallelogram?

\newline

\underline{\hspace{1cm}}^\circ,

\underline{\hspace{1cm}}^\circ,

\underline{\hspace{1cm}}^\circ

Posted 6 months ago

Question

One angle of a triangle measures

110^\circ

. The other two angles are in a ratio of

2:5

. What are the measures of those two angles?

\newline

\underline{\hspace{1cm}}^\circ

\underline{\hspace{1cm}}^\circ

Posted 6 months ago

Question

Three of the angles in a quadrilateral measure

268^\circ,

27^\circ

52^\circ

. What is the measure of the fourth angle?

\newline

\underline{\hspace{1cm}}^\circ

Posted 6 months ago

Question

A circle in the

x y

-plane has the equation

\newline

(x+17.5)^{2}+(y-15 . \overline{3})^{2}=18.1

\newline

Which of the following best describes the location of the center of the circle and the length of its radius?

\newline

1

\newline

(-17.5,15 . \overline{3})

\newline

\sqrt{18.1}

\newline

(-17.5,15 . \overline{3})

\newline

18

1

\newline

(17.5,-15 . \overline{3})

\newline

\sqrt{18.1}

\newline

(17.5,-15 . \overline{3})

\newline

18

1

Posted 8 months ago

Question

Select the type of cross section formed when a right cylinder is cut parallel to its base.

\newline

\newline

\newline

\newline

Posted 7 months ago

Question

Select the type of cross section formed when a sphere is cut by a vertical plane.

\newline

\newline

\newline

\newline

Posted 6 months ago

Question

What is the formula to find the perimeter of a rectangle?

\newline

P=l \cdot w

\newline

P=l+w

\newline

P=2(l+w)

\newline

P=2 l+w

Posted 6 months ago

Question

Find the common ratio of the geometric sequence

-9,-72,-576, \ldots

\newline

Posted 6 months ago

Question

\newline

\log _{8} \frac{1}{8}

\newline

Write your answer in simplest form.

Posted 2 months ago

Question

Jonah measured a summer camp and made a scale drawing. In real life, the sand volleyball court is

8

meters wide. It is

2

centimeters wide in the drawing. What is the scale factor of the drawing? Simplify your answer and write it as a fraction.

Posted 1 hour ago

View all (10384)

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant