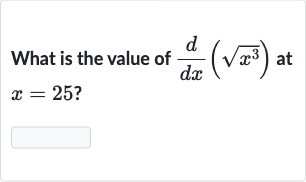AI tutor
Full solution
Q. What is the value of at ?
- Rewrite function: We need to find the derivative of the function with respect to . The function can be rewritten as .
- Apply chain rule: To differentiate , we will use the chain rule. The chain rule states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function.
- Find outer function derivative: The outer function is and the inner function is . We will first find the derivative of the outer function, .
- Find inner function derivative: Next, we find the derivative of the inner function, .
- Apply chain rule again: Now we apply the chain rule: . Substituting the derivatives we found, we get .
- Simplify expression: Simplify the expression: .
- Rewrite with single exponent: Rewrite the expression with a single exponent: .
- Evaluate derivative at : Now we evaluate the derivative at : .
- Calculate final value: Since the square root of is , we have .
- Calculate final value: Since the square root of is , we have .Finally, we calculate the value: .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help