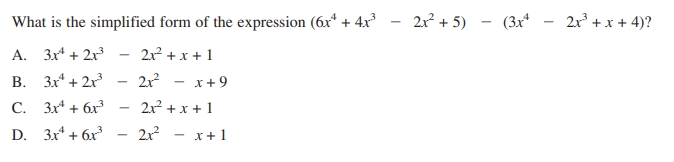What is the simplified form of the expression (6x^(4)+4x^(3)-2x^(2)+5)-(3x^(4)-2x^(3)+x+4) ? A. 3x^(4)+2x^(3)-2x^(2)+x+1 B. 3x^(4)+2x^(3)-2x^(2)-x+9 C. 3x^(4)+6x^(3)-2x^(2)+x+1 D. 3x^(4)+6x^(3)-2x^(2)-x+1

Question

What is the simplified form of the expression  (6x^(4)+4x^(3)-2x^(2)+5)-(3x^(4)-2x^(3)+x+4) ? A.  3x^(4)+2x^(3)-2x^(2)+x+1 B.  3x^(4)+2x^(3)-2x^(2)-x+9 C.  3x^(4)+6x^(3)-2x^(2)+x+1 D.  3x^(4)+6x^(3)-2x^(2)-x+1

Bytelearn · Accepted Answer

Subtract and Combine Like Terms: Subtract the second polynomial from the first by combining like terms. This means subtracting the coefficients of the same powers of x in the second polynomial from the corresponding coefficients in the first polynomial. (6x^(4)+4x^(3)-2x^(2)+5) - (3x^(4)-2x^(3)+x+4) = (6x^(4) - 3x^(4)) + (4x^(3) - (-2x^(3))) - (2x^(2) - 0) + (5 - x) - 4Calculate Coefficients for Each Power: Calculate the coefficients for each power of x. For x^(4): 6x^(4) - 3x^(4) = 3x^(4) For x^(3): 4x^(3) - (-2x^(3)) = 4x^(3) + 2x^(3) = 6x^(3) For x^(2): -2x^(2) - 0 = -2x^(2) For x: 0 - x = -x For the constant term: 5 - 4 = 1Write Simplified Expression: Combine the results from the previous step to write the simplified expression. 3x^(4) + 6x^(3) - 2x^(2) - x + 1Compare with Options: Compare the simplified expression with the given options to find the correct answer. The simplified expression is 3x^(4) + 6x^(3) - 2x^(2) - x + 1, which matches option D.

What is the simplified form of the expression $\newline$ $(6x^{4}+4x^{3}-2x^{2}+5)-(3x^{4}-2x^{3}+x+4)$ ? $\newline$ A. $3x^{4}+2x^{3}-2x^{2}+x+1$ $\newline$ B. $3x^{4}+2x^{3}-2x^{2}-x+9$ $\newline$ C. $3x^{4}+6x^{3}-2x^{2}+x+1$ $\newline$ D. $3x^{4}+6x^{3}-2x^{2}-x+1$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics