AI tutor
Full solution
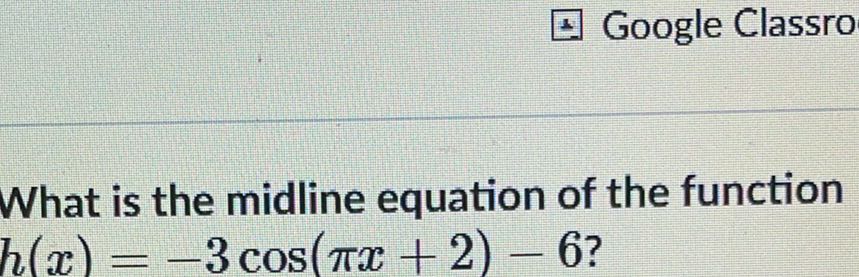
Q. What is the midline equation of the function
- Definition of Midline: The midline of a cosine function is the horizontal line that represents the average value of the function, or the vertical shift from the standard position of the cosine function.
- Identifying Vertical Shift: To find the midline, we look at the vertical shift of the function. The general form of a cosine function with a vertical shift is , where represents the vertical shift.
- Vertical Shift Calculation: In the given function , the vertical shift is represented by the at the end of the function.
- Equation of Midline: Therefore, the equation of the midline is simply , which is a horizontal line at the value of the vertical shift.