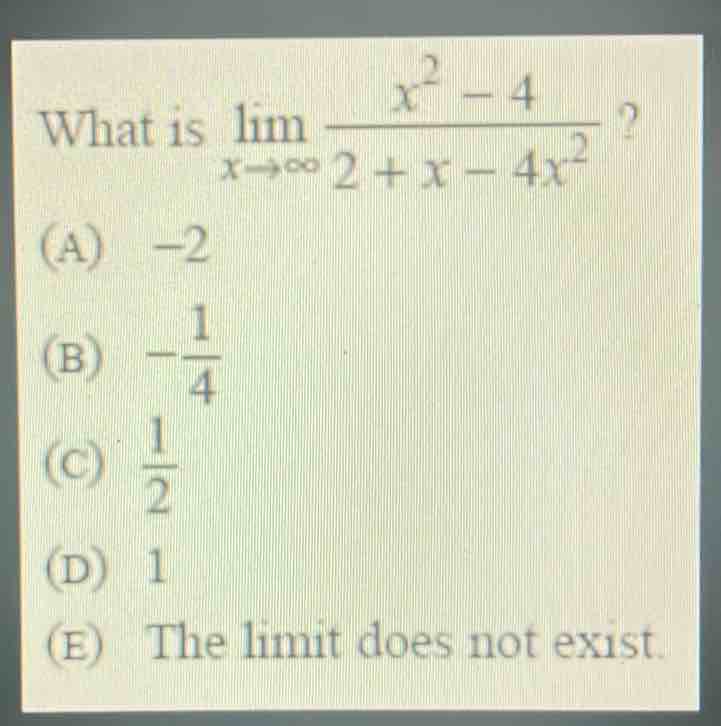Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

What is
lim_(x rarr oo)(x^(2)-4)/(2+x-4x^(2))?
(A) -2
(B)
-(1)/(4)
(C)
(1)/(2)
(D) 1
(E) The limit does not exist.

What is $\lim _{x \rightarrow \infty} \frac{x^{2}-4}{2+x-4 x^{2}} ?$ $\newline$ (A) $-2$ $\newline$ (B) $-\frac{1}{4}$ $\newline$ (C) $\frac{1}{2}$ $\newline$ (D) $1$ $\newline$ (E) The limit does not exist.

View step-by-step help

View step-by-step help

Find derivatives of logarithmic functions

Full solution

Q. What is

\lim _{x \rightarrow \infty} \frac{x^{2}-4}{2+x-4 x^{2}} ?

\newline

(A)

-2

\newline

(B)

-\frac{1}{4}

\newline

(C)

\frac{1}{2}

\newline

(D)

1

\newline

(E) The limit does not exist.

Identify Power Levels: Identify the highest power of $x$ in the numerator and the denominator to simplify the expression. $\newline$ Numerator highest power: $x^2$ $\newline$ Denominator highest power: $-4x^2$
Simplify by Division: Simplify the expression by dividing both the numerator and the denominator by $x^2$ . $\newline$ $\lim_{x \to \infty} \left[\frac{x^2}{x^2} - \frac{4}{x^2}\right] / \left[\frac{2}{x^2} + \frac{x}{x^2} - \frac{4x^2}{x^2}\right]$ $\newline$ $= \lim_{x \to \infty} \left[1 - 0\right] / \left[0 + 0 - 4\right]$ $\newline$ $= \lim_{x \to \infty} \frac{1}{-4}$
Calculate Final Limit: Calculate the final limit. $\lim_{x \rightarrow \infty} \frac{1}{-4} = -\frac{1}{4}$

More problems from Find derivatives of logarithmic functions

Question

Find the derivative of

f(x)

\newline

f(x) = \cos(x)

\newline

f'(x) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \ln(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan^{-1}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = x e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \frac{e^x}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^{(x + 1)}

\newline

f'\left(x\right) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \sqrt{x+3}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

g(x)

\newline

g(x) = \ln(2x)

\newline

g^{\prime}(x) =

Posted 3 months ago