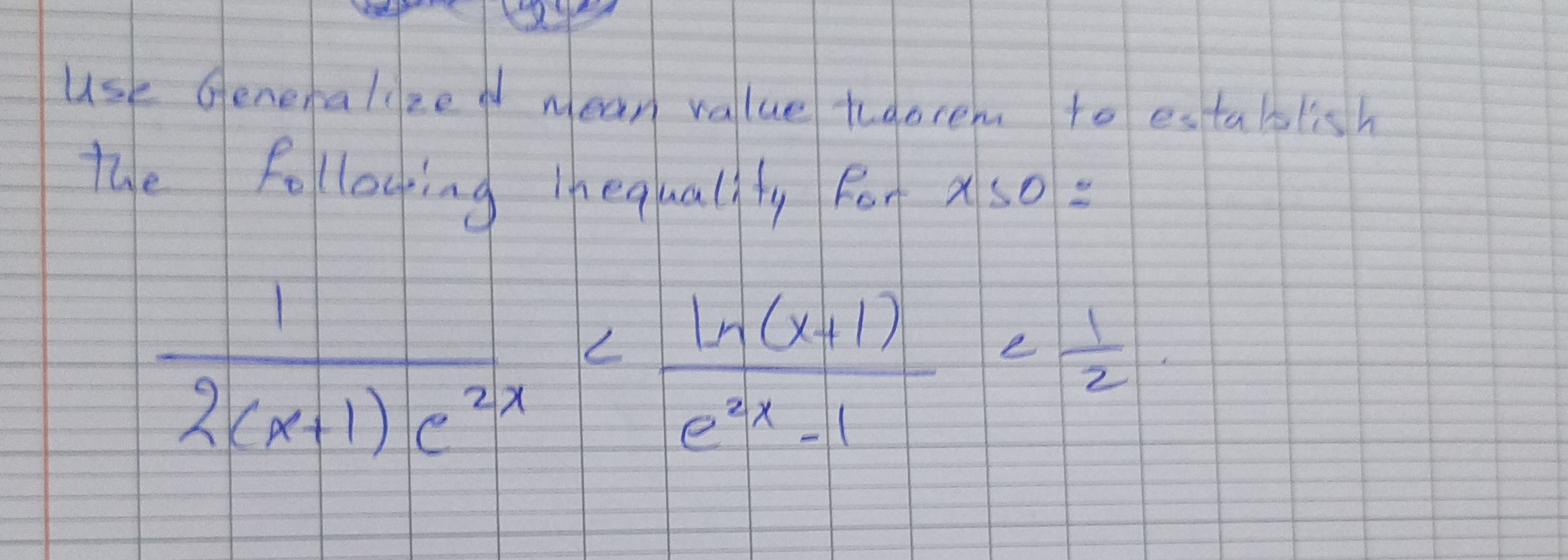Use Genenalized mean value twoorem to estalslish the following inequality for $x 50$ : $\newline$ $\frac{1}{2(x+1) e^{2 x}}<\frac{\ln (x+1)}{e^{2 x}-1}<\frac{1}{2}$

View step-by-step help

Home

Math Problems

Algebra 1

Simplify exponential expressions using exponent rules

Full solution

Q. Use Genenalized mean value twoorem to estalslish the following inequality for

x 50

\newline

\frac{1}{2(x+1) e^{2 x}}<\frac{\ln (x+1)}{e^{2 x}-1}<\frac{1}{2}

Introduction: Let's consider two functions $f(x)$ and $g(x)$ that are continuous on the closed interval $[a, b]$ and differentiable on the open interval $(a, b)$ . The Generalized Mean Value Theorem (also known as Cauchy's Mean Value Theorem) states that there exists some $c$ in $(a, b)$ such that: $\newline$ $(f(b) - f(a)) / (g(b) - g(a)) = f'(c) / g'(c)$ $\newline$ For our problem, we need to choose appropriate $f(x)$ and $g(x)$ to apply the theorem. Let's take $f(x) = \ln(x+1)$ and $g(x) = e^{2x} - 1$ . We will apply the theorem on the interval $g(x)$ $0$ for $g(x)$ $1$ .
Verification of Conditions: First, we need to verify that $f(x)$ and $g(x)$ satisfy the conditions of the theorem. The function $f(x) = \ln(x+1)$ is continuous and differentiable for $x > 0$ , and $g(x) = e^{2x} - 1$ is also continuous and differentiable for all $x$ since the exponential function is continuous and differentiable everywhere. Thus, the conditions are satisfied.
Derivative Calculation: Now, let's calculate the derivatives $f'(x)$ and $g'(x)$ . For $f(x) = \ln(x+1)$ , the derivative is $f'(x) = \frac{1}{(x+1)}$ . For $g(x) = e^{2x} - 1$ , the derivative is $g'(x) = 2e^{2x}$ .
Applying Generalized Mean Value Theorem: Applying the Generalized Mean Value Theorem, we get: $\newline$ $\frac{\ln(x+1) - \ln(1)}{e^{2x} - e^{0}} = \frac{1/(c+1)}{2e^{2c}}$ $\newline$ Simplifying the left side, we have: $\newline$ $\frac{\ln(x+1)}{e^{2x} - 1} = \frac{1/(c+1)}{2e^{2c}}$ $\newline$ Now, we need to find the bounds for the right side of the equation.
Finding Bounds: Since $c$ is in the interval $(0, x)$ , we know that $c > 0$ . Therefore, $c+1 > 1$ and $e^{2c} > e^{0} = 1$ . This means that $\frac{1}{c+1} < 1$ and $2e^{2c} > 2$ . So, the fraction $\frac{1}{c+1} / 2e^{2c}$ is less than $\frac{1}{2}$ .
Finding Bounds: Since $c$ is in the interval $(0, x)$ , we know that $c > 0$ . Therefore, $c+1 > 1$ and $e^{2c} > e^{0} = 1$ . This means that $\frac{1}{c+1} < 1$ and $2e^{2c} > 2$ . So, the fraction $\frac{1}{c+1} / (2e^{2c})$ is less than $\frac{1}{2}$ .On the other hand, as $c$ approaches $(0, x)$ $0$ from the right, $(0, x)$ $1$ approaches $(0, x)$ $2$ and $(0, x)$ $3$ approaches $(0, x)$ $4$ , so the fraction $\frac{1}{c+1} / (2e^{2c})$ approaches $\frac{1}{2}$ from the left. Therefore, we have: $\newline$ $(0, x)$ $7$ $\newline$ Since $(0, x)$ $8$ , we can conclude that: $\newline$ $(0, x)$ $9$