Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

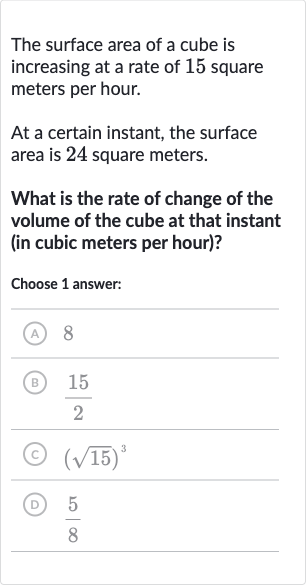
The surface area of a cube is increasing at a rate of 15 square meters per hour. At a certain instant, the surface area is 24 square meters. What is the rate of change of the volume of the cube at that instant (in cubic meters per hour)? Choose 1 answer: (A) 8 (B) (15)/(2) (C) (sqrt15)^(3) (D) (5)/(8)

The surface area of a cube is increasing at a rate of 1515 square meters per hour.\newlineAt a certain instant, the surface area is 2424 square meters.\newlineWhat is the rate of change of the volume of the cube at that instant (in cubic meters per hour)?\newlineChoose 11 answer:\newline(A) 88\newline(B) 152 \frac{15}{2} \newline(C) (15)3 (\sqrt{15})^{3} \newline(D) 58 \frac{5}{8}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 6right chevron icon
Volume of cubes and rectangular prisms: word problemsright chevron icon

Full solution

Q. The surface area of a cube is increasing at a rate of 1515 square meters per hour.\newlineAt a certain instant, the surface area is 2424 square meters.\newlineWhat is the rate of change of the volume of the cube at that instant (in cubic meters per hour)?\newlineChoose 11 answer:\newline(A) 88\newline(B) 152 \frac{15}{2} \newline(C) (15)3 (\sqrt{15})^{3} \newline(D) 58 \frac{5}{8}
  1. Surface Area Calculation: The surface area of a cube is 66 times one of its side's square, so one side's square is 24 m26\frac{24 \, \text{m}^2}{6}.\newlineCalculate the length of one side.\newlineSide length = 24 m26=4 m2=2 m\sqrt{\frac{24 \, \text{m}^2}{6}} = \sqrt{4 \, \text{m}^2} = 2 \, \text{m}.
  2. Volume Calculation: The volume of a cube is side length cubed, V=s3V = s^3. Calculate the volume with the side length. Volume = 2 m×2 m×2 m=8 m32 \, \text{m} \times 2 \, \text{m} \times 2 \, \text{m} = 8 \, \text{m}^3.
  3. Surface Area Rate of Change: The surface area is increasing at a rate of 15 m2/hour15 \, \text{m}^2/\text{hour}. Since the surface area is 6×side length26 \times \text{side length}^2, d(SA)dt=6×2×side length×d(side length)dt\frac{d(SA)}{dt} = 6 \times 2 \times \text{side length} \times \frac{d(\text{side length})}{dt}.
  4. Side Length Rate of Change: Solve for d(side length)dt\frac{d(\text{side length})}{dt}.15 m2/hour=6×2×2 m×d(side length)dt15 \, \text{m}^2/\text{hour} = 6 \times 2 \times 2 \, \text{m} \times \frac{d(\text{side length})}{dt}.d(side length)dt=15 m2/hour(6×2×2 m)=15 m2/hour24 m=58 m/hour\frac{d(\text{side length})}{dt} = \frac{15 \, \text{m}^2/\text{hour}}{(6 \times 2 \times 2 \, \text{m})} = \frac{15 \, \text{m}^2/\text{hour}}{24 \, \text{m}} = \frac{5}{8} \, \text{m/hour}.
  5. Volume Rate of Change: The rate of change of the volume is given by dVdt=3×side length2×d(side length)dt\frac{dV}{dt} = 3 \times \text{side length}^2 \times \frac{d(\text{side length})}{dt}. Calculate dVdt\frac{dV}{dt} using the side length and d(side length)dt\frac{d(\text{side length})}{dt}. dVdt=3×(2 m)2×(58 m/hour)=3×4 m2×58 m/hour=152 m3/hour.\frac{dV}{dt} = 3 \times (2 \, \text{m})^2 \times \left(\frac{5}{8} \, \text{m/hour}\right) = 3 \times 4 \, \text{m}^2 \times \frac{5}{8} \, \text{m/hour} = \frac{15}{2} \, \text{m}^3/\text{hour}.

More problems from Volume of cubes and rectangular prisms: word problems

Question
Chinedu was given this problem:\newlineA person stands at a distance of 1818 meters east of an intersection and watches a car driving away from the intersection to the north at 33 meters per second. The function y(t) y(t) gives the car's distance, in meters, north of the intersection at time t t . At a certain instant t0 t_{0} , the angle θ(t0) \theta\left(t_{0}\right) between the line of sight from the person to the car and the line of sight from the person to the intersection is 00.77 radians. What is the rate of change of the angle θ(t) \theta(t) at that instant?\newlineWhich equation should Chinedu use to solve the problem?\newlineChoose 11 answer:\newline(A) tan⁡[θ(t)]=y(t)18 \tan [\theta(t)]=\frac{y(t)}{18} \newline(B) θ(t)=18⋅y(t)2 \theta(t)=\frac{18 \cdot y(t)}{2} \newline(C) θ(t)+18+y(t)=180 \theta(t)+18+y(t)=180 \newline(D) [θ(t)]2=182+[y(t)]2 [\theta(t)]^{2}=18^{2}+[y(t)]^{2}
Get tutor helpright-arrow

Posted 3 months ago

Question
Steve was given this problem:\newlineThe radius r(t) r(t) of a circle is increasing at a rate of 33 centimeters per second. At a certain instant t0 t_{0} , the radius is 88 centimeters. What is the rate of change of the area A(t) A(t) of the circle at that instant?\newlineWhich equation should Steve use to solve the problem?\newlineChoose 11 answer:\newline(A) A(t)=2π⋅r(t) A(t)=2 \pi \cdot r(t) \newline(B) A(t)=π[r(t)]2 A(t)=\pi[r(t)]^{2} \newline(C) A(t)=4π[r(t)]2 A(t)=4 \pi[r(t)]^{2} \newline(D) A(t)=43π[r(t)]3 A(t)=\frac{4}{3} \pi[r(t)]^{3}
Get tutor helpright-arrow

Posted 3 months ago

Question
Benjamin invests $400 \$ 400 in a savings account that earns 5% 5 \% interest each year.\newlineWhich expression gives the balance in the account after 33 years?\newlineChoose 11 answer:\newline(A) 400⋅0.05⋅0.05⋅0.05 400 \cdot 0.05 \cdot 0.05 \cdot 0.05 \newline(B) 400+(1+0.05)(1+0.05)(1+0.05) 400+(1+0.05)(1+0.05)(1+0.05) \newline(C) 400+0.05⋅0.05⋅0.05 400+0.05 \cdot 0.05 \cdot 0.05 \newline(D) 400(1+0.05)(1+0.05)(1+0.05) 400(1+0.05)(1+0.05)(1+0.05)
Get tutor helpright-arrow

Posted 3 months ago

Question
Workbook Question #1010\newlineThis solid has curved sides. All cross sections parallel to the base are squares measuring 33 units on each side. The height from the base to the top is 1010 units. What is the volume of this solid?\newlinea. 3030 cubic units\newlineb. 6060 cubic units\newlinec. 9090 cubic units\newlined. There is not enough information to determine the volume.
Get tutor helpright-arrow

Posted 2 months ago

Question
Complet the \newlineT chart of values for the Exponential equation. Round to the nearest 10th10^{th} if necessary.\newlineWhen you have checked your quiz and know that your T-Chart is correct, graph this Exponential equation and upload it (along with the others) to the Absolute Value and Exponential Graph Upload Assignment for points\newliney=−3x−4y=-3^{x}-4\newline\newlinexx\newlineyy\newline\newline00\newline\newline11\newline\newline22\newline\newline33\newline\newline−1-1\newline\newline−2-2
Get tutor helpright-arrow

Posted 2 months ago

Question
Directions: Type your answer in the box.\newlineWhat is the volume of a square-based pyramid with base side length of 88 inches and a height of 1212 inches? Write your answer in the box provided.\newlineIi3Ii^{3}
Get tutor helpright-arrow

Posted 2 months ago

Question
Submit Answer\newline−11 Points-\frac{1}{1} \text{ Points}\newlineDETAILS\newlineLARCALCET88 77.R.025025.\newlineUse the disk method to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the \newlinex-axis.\newliney=11+x2,y=0,x=−1,x=1y=\frac{1}{\sqrt{1+x^{2}}},\quad y=0,\quad x=-1,\quad x=1\newlineSubmit Answer\newline−11 Points-\frac{1}{1} \text{ Points}\newlineDETAILS\newlineLARCALCET88 77.R.027027.
Get tutor helpright-arrow

Posted 2 months ago

Question
Burlington Paper Goods is considering purchasing a new delivery truck. Burlingten uses the average rate of return method to evaluate capital asset decisions.\newlineIf the initial cost of the truck is $67,000\$67,000 with a salvage value of $7,000\$7,000, and it has a before tax average annual net cash flow of $30,000\$30,000 and an annual depreciation of $15,000\$15,000, what is the average rate of retum on the truck? Asaume a 35%35\% tax rate.\newlinea) 26.35%26.35\%\newlineb) 37.23%37.23\%\newlinec) 42.59%42.59\%\newlined) 18.27%18.27\%
Get tutor helpright-arrow

Posted 2 months ago

Question
A rectangular prism has a height of 7 in7\,\text{in} and the base with dimensions of 8 in8\,\text{in} by 6 in6\,\text{in}. What is the lateral area, in square inches?
Get tutor helpright-arrow

Posted 2 months ago

Question
[33/66 Points]\newlineDETAILS\newlinePREVIOUS ANSWERS\newlineLARCOLALG1010 33.11.071071.\newlineMYNOTES\newlineThe total revenue RR earned (in thousands of dollars) from manufacturing handheld video games is given by R(p)=−25p2+1700pR(p)=-25p^{2}+1700p, where pp is the price per unit\newline(a) Find the revenues when the prices per unit are $20\$20, $25\$25, and $30\$30.\newlineR($20)$24000R(\$20)\quad\$24000\newlinethousand\newlineR($25)$26875R(\$25)\quad\$26875\newline\checkmark thousand\newlineR($30)$28500R(\$30)\quad\$28500\newline\checkmark thousand\newline(b) Find the unit price that yields a maximum revenue.\newlineper unit\newlineWhat is the maximum revenue?\newline$\$\quad\newlinethousand\newlineEnter an exast number.\newlineExplain.
Get tutor helpright-arrow

Posted 2 months ago

View all (18)