Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

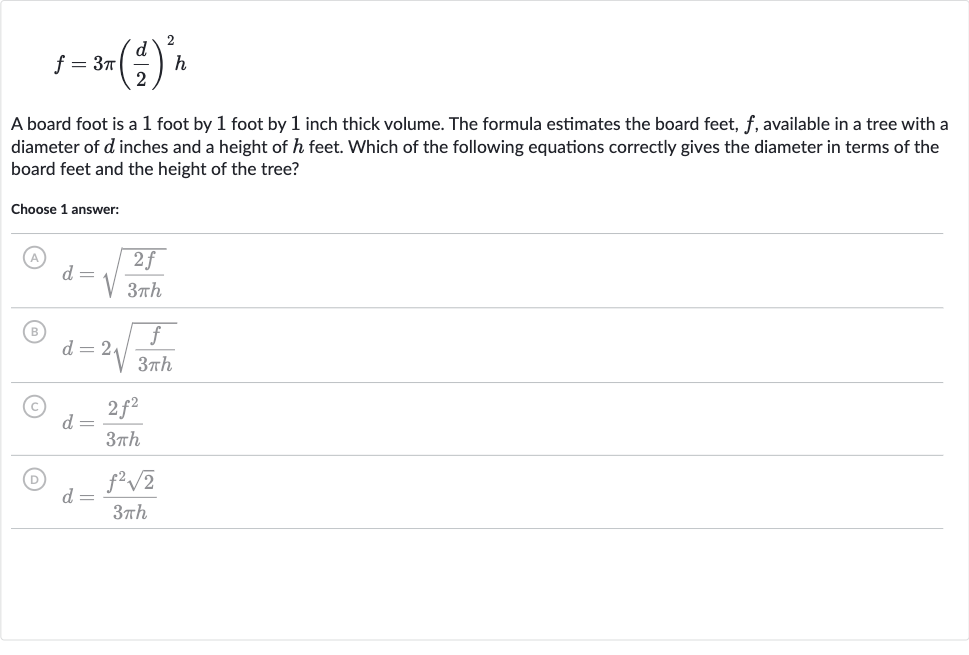
f=3pi((d)/(2))^(2)h
A board foot is a 1 foot by 1 foot by 1 inch thick volume. The formula estimates the board feet,
f, available in a tree with a diameter of
d inches and a height of
h feet. Which of the following equations correctly gives the diameter in terms of the board feet and the height of the tree?
Choose 1 answer:
(A)
d=sqrt((2f)/(3pi h))
(B)
d=2sqrt((f)/(3pi h))
(C)
d=(2f^(2))/(3pi h)
(D)
d=(f^(2)sqrt2)/(3pi h)

$f=3 \pi\left(\frac{d}{2}\right)^{2} h$ $\newline$ A board foot is a $1$ foot by $1$ foot by $1$ inch thick volume. The formula estimates the board feet, $f$ , available in a tree with a diameter of $d$ inches and a height of $h$ feet. Which of the following equations correctly gives the diameter in terms of the board feet and the height of the tree? $\newline$ Choose $1$ answer: $\newline$ (A) $d=\sqrt{\frac{2 f}{3 \pi h}}$ $\newline$ (B) $d=2 \sqrt{\frac{f}{3 \pi h}}$ $\newline$ (C) $d=\frac{2 f^{2}}{3 \pi h}$ $\newline$ (D) $d=\frac{f^{2} \sqrt{2}}{3 \pi h}$

View step-by-step help

View step-by-step help

Volume of cubes and rectangular prisms: word problems

Full solution

Q.

f=3 \pi\left(\frac{d}{2}\right)^{2} h

\newline

A board foot is a

1

foot by

1

foot by

1

inch thick volume. The formula estimates the board feet,

f

, available in a tree with a diameter of

d

inches and a height of

h

feet. Which of the following equations correctly gives the diameter in terms of the board feet and the height of the tree?

\newline

Choose

1

answer:

\newline

(A)

d=\sqrt{\frac{2 f}{3 \pi h}}

\newline

(B)

d=2 \sqrt{\frac{f}{3 \pi h}}

\newline

(C)

d=\frac{2 f^{2}}{3 \pi h}

\newline

(D)

d=\frac{f^{2} \sqrt{2}}{3 \pi h}

Isolate $(\frac{d}{2})^2$ : We have the original formula: $f = 3\pi\left(\left(\frac{d}{2}\right)^2\right)h$ . We need to solve for $d$ .
Solve for $d/2$ : First, divide both sides by $3\pi h$ to isolate $(d/2)^2$ on one side: $(d/2)^2 = \frac{f}{3\pi h}$ .
Solve for d: Next, take the square root of both sides to solve for $d/2$ : $d/2 = \sqrt{f/(3\pi h)}$ .
Solve for d: Next, take the square root of both sides to solve for $d/2$ : $d/2 = \sqrt{f/(3\pi h)}$ . Finally, multiply both sides by $2$ to solve for d: $d = 2\sqrt{f/(3\pi h)}$ .

More problems from Volume of cubes and rectangular prisms: word problems

Question

Chinedu was given this problem:

\newline

A person stands at a distance of

18

meters east of an intersection and watches a car driving away from the intersection to the north at

3

meters per second. The function

y(t)

gives the car's distance, in meters, north of the intersection at time

t

. At a certain instant

t_{0}

\theta\left(t_{0}\right)

between the line of sight from the person to the car and the line of sight from the person to the intersection is

0

7

radians. What is the rate of change of the angle

\theta(t)

at that instant?

\newline

Which equation should Chinedu use to solve the problem?

\newline

1

\newline

\tan [\theta(t)]=\frac{y(t)}{18}

\newline

\theta(t)=\frac{18 \cdot y(t)}{2}

\newline

\theta(t)+18+y(t)=180

\newline

[\theta(t)]^{2}=18^{2}+[y(t)]^{2}

Posted 9 months ago

Question

Steve was given this problem:

\newline

r(t)

of a circle is increasing at a rate of

3

centimeters per second. At a certain instant

t_{0}

, the radius is

8

centimeters. What is the rate of change of the area

A(t)

of the circle at that instant?

\newline

Which equation should Steve use to solve the problem?

\newline

1

\newline

A(t)=2 \pi \cdot r(t)

\newline

A(t)=\pi[r(t)]^{2}

\newline

A(t)=4 \pi[r(t)]^{2}

\newline

A(t)=\frac{4}{3} \pi[r(t)]^{3}

Posted 9 months ago

Question

Benjamin invests

\$ 400

in a savings account that earns

5 \%

interest each year.

\newline

Which expression gives the balance in the account after

3

\newline

1

\newline

400 \cdot 0.05 \cdot 0.05 \cdot 0.05

\newline

400+(1+0.05)(1+0.05)(1+0.05)

\newline

400+0.05 \cdot 0.05 \cdot 0.05

\newline

400(1+0.05)(1+0.05)(1+0.05)

Posted 9 months ago

Question

f(x)=\frac{x+1}{xe^{x}+e^{x}}

x\neq-1

\newline

f

is continuous for all real numbers.

\newline

f(-1)

\newline

1

\newline

1

\newline

e

\newline

2

Posted 8 months ago

Question

v=\sqrt{\frac{3 R T}{M}}

\newline

The root-mean-square speed is the measure of the speed of particles in a gas. Root-mean-square speed,

v

, can be calculated using the equation shown, where

M

is the molar mass of a gas,

R

is the molar gas constant, and

T

is the temperature. Which of the following equations correctly expresses the molar mass of a gas in terms of root-mean-square speed, temperature, and the molar gas constant?

\newline

1

\newline

M=\left(\frac{3 R T}{v}\right)^{2}

\newline

M=\frac{3 R T}{(v)^{2}}

\newline

M=\frac{(v)^{2}}{3 R T}

\newline

M=\frac{\sqrt{3 R T}}{v}

Posted 7 months ago

Question

The surface area of a cylinder is increasing at a rate of

9 \pi

square meters per hour.

\newline

The height of the cylinder is fixed at

3

\newline

At a certain instant, the surface area is

36 \pi

\newline

What is the rate of change of the volume of the cylinder at that instant (in cubic meters per hour)?

\newline

1

\newline

9 \pi

\newline

27 \pi

\newline

\frac{\pi}{3}

\newline

\frac{1}{2}

\newline

The surface area of a cylinder with base radius

r

h

2 \pi r^{2}+2 \pi r h

\newline

The volume of a cylinder with base radius

r

h

\pi r^{2} h

Posted 7 months ago

Question

The radius of the base of a cone is increasing at a rate of

10

meters per second.

\newline

The height of the cone is fixed at

6

\newline

At a certain instant, the radius is

1

\newline

What is the rate of change of the volume of the cone at that instant (in cubic meters per second)?

\newline

1

\newline

20 \pi

\newline

40 \pi

\newline

400 \pi

\newline

200 \pi

\newline

The volume of a cone with radius

r

h

\pi r^{2} \frac{h}{3}

Posted 7 months ago

Question

The side of the base of a square prism is increasing at a rate of

5

meters per second and the height of the prism is decreasing at a rate of

2

meters per second.

\newline

At a certain instant, the base's side is

6

meters and the height is

7

\newline

What is the rate of change of the volume of the prism at that instant (in cubic meters per second)?

\newline

1

\newline

492

\newline

-492

\newline

-348

\newline

348

\newline

The volume of a square prism with base side

s

h

s^{2} h

Posted 7 months ago

Question

The side of the base of a square pyramid is increasing at a rate of

6

meters per minute and the height of the pyramid is decreasing at a rate of

1

meter per minute.

\newline

At a certain instant, the base's side is

3

meters and the height is

9

\newline

What is the rate of change of the volume of the pyramid at that instant (in cubic meters per minute)?

\newline

1

\newline

-111

\newline

\mathbf{1 1 1}

\newline

-105

\newline

105

\newline

The volume of a square pyramid with base side

s

h

\frac{1}{3} s^{2} h

Posted 7 months ago

Question

You pick a card at random, put it back, and then pick another card at random.

\newline

4

\newline

5

\newline

6

\newline

7

\newline

What is the probability of picking a number greater than

5

and then picking a

4

\newline

Write your answer as a percentage.

Posted 1 month ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant