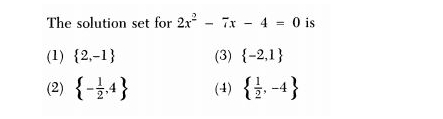AI tutor
Full solution
Q. The solution set for is:() () () ()
- Identify Equation Type: Step : Identify the type of equation and its standard form.The equation is a quadratic equation in the standard form , where , , and .
- Use Quadratic Formula: Step : Use the quadratic formula to find the roots.The quadratic formula is . Plugging in the values:
- Simplify Square Root: Step : Simplify the square root and solve for . or or or