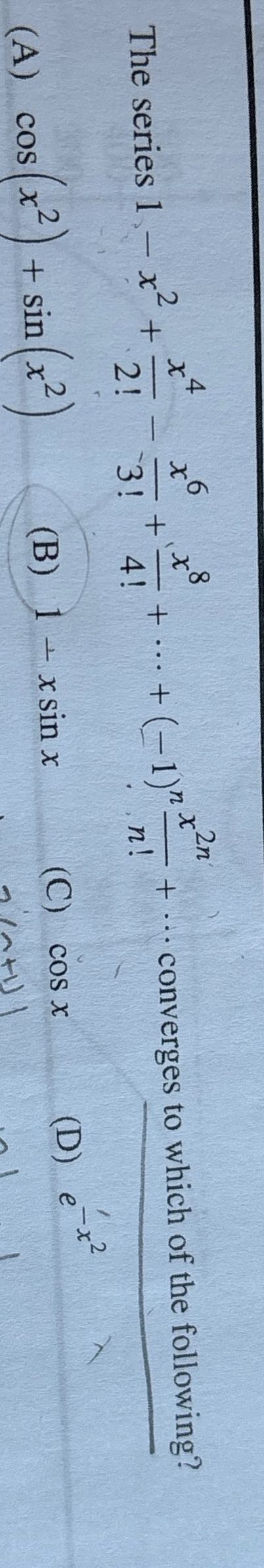Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

The series
1-x^(2)+(x^(4))/(2!)-(x^(6))/(3!)+(x^(8))/(4!)+cdots+(-1)^(n)(x^(2n))/(n!)+cdots converges to which of the following?
(A)
cos(x^(2))+sin(x^(2))
(B)
1+x sin x
(C)
cos x
(D)
e^(-x^(2))

The series $1-x^{2}+\frac{x^{4}}{2!}-\frac{x^{6}}{3!}+\frac{x^{8}}{4!}+\cdots+(-1)^{n} \frac{x^{2 n}}{n!}+\cdots$ converges to which of the following? $\newline$ (A) $\cos \left(x^{2}\right)+\sin \left(x^{2}\right)$ $\newline$ (B) $1+x \sin x$ $\newline$ (C) $\cos x$ $\newline$ (D) $e^{-x^{2}}$

View step-by-step help

View step-by-step help

Find derivatives of using multiple formulae

Full solution

Q. The series

1-x^{2}+\frac{x^{4}}{2!}-\frac{x^{6}}{3!}+\frac{x^{8}}{4!}+\cdots+(-1)^{n} \frac{x^{2 n}}{n!}+\cdots

converges to which of the following?

\newline

(A)

\cos \left(x^{2}\right)+\sin \left(x^{2}\right)

\newline

(B)

1+x \sin x

\newline

(C)

\cos x

\newline

(D)

e^{-x^{2}}

Identify general term: Identify the general term of the series. $\newline$ The general term of the series is $(-1)^n(x^{2n})/(n!)$ . This resembles the Taylor series expansion of $e^{x}$ but with $x$ replaced by $-x^2$ .
Recognize represented function: Recognize the function represented by the series. The series is the Taylor series for $e^{-x^2}$ , since replacing $x$ in the $e^{x}$ series with $-x^2$ gives us the terms of the given series.
Match series to function: Match the series to the correct function from the options. $\newline$ The series matches the Taylor series for $e^{(-x^2)}$ , which is option $(D)$ .

More problems from Find derivatives of using multiple formulae

Question

Find the derivative of

f(x)

\newline

f(x) = \cos(x)

\newline

f'(x) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \ln(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan^{-1}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = x e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \frac{e^x}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^{(x + 1)}

\newline

f'\left(x\right) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \sqrt{x+3}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

g(x)

\newline

g(x) = \ln(2x)

\newline

g^{\prime}(x) =

Posted 3 months ago