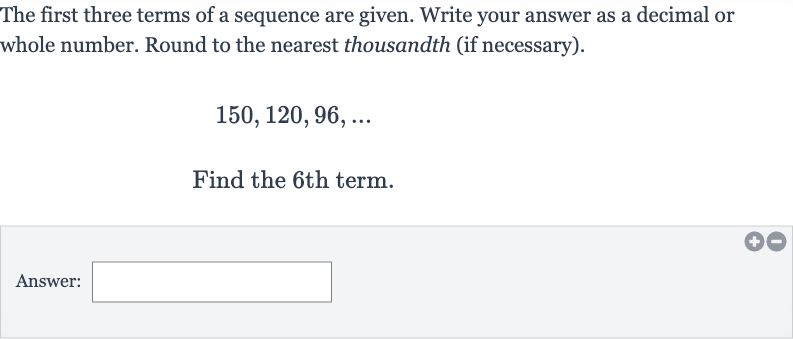
The first three terms of a sequence are given. Write your answer as a decimal or whole number. Round to the nearest thousandth (if necessary). $\newline$ $150,120,96, \ldots$ $\newline$ Find the $6$ th term. $\newline$ Answer:

Full solution

Q. The first three terms of a sequence are given. Write your answer as a decimal or whole number. Round to the nearest thousandth (if necessary).

\newline

150,120,96, \ldots

\newline

Find the

6

th term.

\newline

Answer:

Identify Pattern: Identify the pattern in the sequence. $\newline$ We need to determine the pattern by which the sequence is generated. By looking at the given terms, we can see that each term is a certain percentage of the previous term. $\newline$ $\$120$ is $\frac{120}{150} = 0.8$ (or $80\%$ ) of $\$150$ . $\newline$ $\$96$ is $\frac{96}{120} = 0.8$ (or $80\%$ ) of $\$120$ . $\newline$ This suggests that each term is $80\%$ of the previous term, which means the sequence is a geometric sequence with a common ratio of $0.8$ .
Use Formula: Use the formula for the nth term of a geometric sequence. $\newline$ The nth term of a geometric sequence can be found using the formula $a_n = a_1 \cdot r^{(n-1)}$ , where $a_1$ is the first term, $r$ is the common ratio, and $n$ is the term number. $\newline$ Here, $a_1 = 150$ , $r = 0.8$ , and we want to find the $6$ th term, so $n = 6$ .
Calculate $6$ th Term: Calculate the $6$ th term. $\newline$ Using the formula, we calculate the $6$ th term as follows: $\newline$ $a_6 = 150 \cdot 0.8^{(6-1)}$ $\newline$ $a_6 = 150 \cdot 0.8^5$ $\newline$ $a_6 = 150 \cdot 0.32768$ $\newline$ $a_6 = 49.152$
Round Answer: Round the answer to the nearest thousandth. $\newline$ The $6$ th term, when rounded to the nearest thousandth, is: $\newline$ $\$$ $a_6 \approx 49.152$ $\$$ $\newline$ Since $49.152$ is already to the nearest thousandth, we do not need to round further.