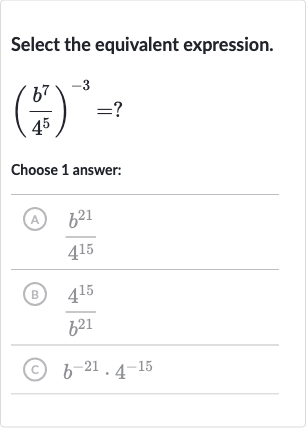
Select the equivalent expression. ((b^(7))/(4^(5)))^(-3)=? Choose 1 answer: (A) (b^(21))/(4^(15)) (B) (4^(15))/(b^(21)) (c) b^(-21)*4^(-15)

Question

Select the equivalent expression.  ((b^(7))/(4^(5)))^(-3)=? Choose 1 answer: (A)  (b^(21))/(4^(15)) (B)  (4^(15))/(b^(21)) (c)  b^(-21)*4^(-15)

Bytelearn · Accepted Answer

Apply negative exponent rule: Apply the negative exponent rule. The negative exponent rule states that a^(-n) = 1/(a^n). Therefore, we can rewrite the expression as the reciprocal of the base raised to the positive exponent. ((b^(7))/(4^(5)))^(-3) = 1/((b^(7))/(4^(5)))^(3)Apply power of quotient rule: Apply the power of a quotient rule. The power of a quotient rule states that (a/b)^n = a^n / b^n. Therefore, we can apply this rule to the expression inside the reciprocal. 1/((b^(7))/(4^(5)))^(3) = 1/((b^(7))^3 / (4^(5))^3)Simplify powers: Simplify the powers. Now we simplify the powers by multiplying the exponents. 1/((b^(7))^3 / (4^(5))^3) = 1/(b^(7*3) / 4^(5*3)) = 1/(b^(21) / 4^(15))Invert fraction: Invert the fraction to remove the reciprocal. To remove the reciprocal, we can invert the fraction. 1/(b^(21) / 4^(15)) = 4^(15) / b^(21)Check answer choices: Check the answer choices. We need to match our result with the given answer choices. 4^(15) / b^(21) corresponds to answer choice (B).

Select the equivalent expression. $\newline$ $\left(\frac{b^{7}}{4^{5}}\right)^{-3}=\,?$ $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{b^{21}}{4^{15}}$ $\newline$ (B) $\frac{4^{15}}{b^{21}}$ $\newline$ (C) $b^{-21}\cdot 4^{-15}$

Full solution

More problems from Evaluate expressions using properties of exponents

Related topics

Select the equivalent expression.\newline(b745)−3= ?\left(\frac{b^{7}}{4^{5}}\right)^{-3}=\,?(45b7​)−3=?\newlineChoose 111 answer:\newline(A) b21415\frac{b^{21}}{4^{15}}415b21​\newline(B) 415b21\frac{4^{15}}{b^{21}}b21415​\newline(C) b−21⋅4−15b^{-21}\cdot 4^{-15}b−21⋅4−15

Select the equivalent expression. $\newline$ $\left(\frac{b^{7}}{4^{5}}\right)^{-3}=\,?$ $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{b^{21}}{4^{15}}$ $\newline$ (B) $\frac{4^{15}}{b^{21}}$ $\newline$ (C) $b^{-21}\cdot 4^{-15}$