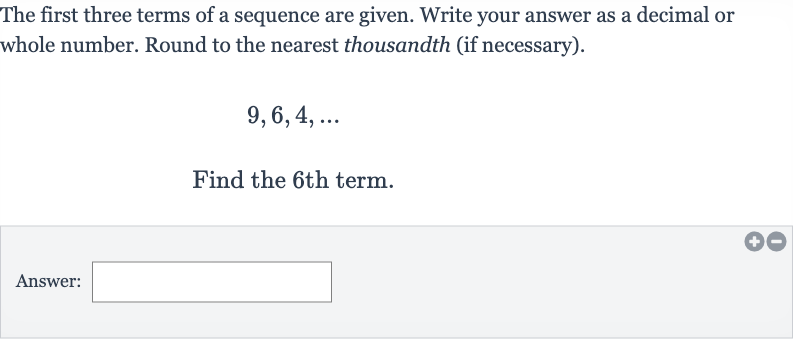
The first three terms of a sequence are given. Write your answer as a decimal or whole number. Round to the nearest thousandth (if necessary). $\newline$ $9,6,4, \ldots$ $\newline$ Find the $6$ th term. $\newline$ Answer:

View step-by-step help

Home

Math Problems

Grade 6

Powers with decimal bases

Full solution

Q. The first three terms of a sequence are given. Write your answer as a decimal or whole number. Round to the nearest thousandth (if necessary).

\newline

9,6,4, \ldots

\newline

Find the

6

th term.

\newline

Answer:

Identify Pattern: Identify the pattern in the sequence. $\newline$ The given sequence is $9, 6, 4, \ldots$ $\newline$ To find the pattern, we look at the differences between consecutive terms. $\newline$ The difference between the first and second term is $6 - 9 = -3$ . $\newline$ The difference between the second and third term is $4 - 6 = -2$ . $\newline$ The differences are not constant, so this is not an arithmetic sequence. $\newline$ We need to look for another type of pattern, such as a geometric sequence or a sequence with a varying difference.
Check Geometric Sequence: Check for a geometric sequence. $\newline$ A geometric sequence is one where each term after the first is found by multiplying the previous term by a constant called the common ratio $r$ . $\newline$ To find the common ratio, we divide the second term by the first term and the third term by the second term. $\newline$ The common ratio between the second and first term is $\frac{6}{9} = \frac{2}{3}$ . $\newline$ The common ratio between the third and second term is $\frac{4}{6} = \frac{2}{3}$ . $\newline$ Since the common ratio is the same for these terms, we can conclude that this is a geometric sequence with a common ratio of $\frac{2}{3}$ .
Use nth Term Formula: Use the formula for the nth term of a geometric sequence to find the $6$ th term. $\newline$ The formula for the nth term $a_n$ of a geometric sequence is $a_n = a_1 \cdot r^{(n-1)}$ , where $a_1$ is the first term and $r$ is the common ratio. $\newline$ The first term $a_1$ is $9$ , the common ratio $r$ is $\frac{2}{3}$ , and we want to find the $6$ th term $n=6$ . $\newline$ So, $a_6 = 9 \cdot \left(\frac{2}{3}\right)^{6-1} = 9 \cdot \left(\frac{2}{3}\right)^5$ .
Calculate $6$ th Term: Calculate the $6$ th term. $\newline$ $a_6 = 9 \times \left(\frac{2}{3}\right)^5$ $\newline$ $a_6 = 9 \times \left(\frac{32}{243}\right)$ (since $2^5 = 32$ and $3^5 = 243$ ) $\newline$ $a_6 = \frac{288}{243}$ $\newline$ $a_6 \approx 1.185$ $\newline$ Since we need to round to the nearest thousandth, the $6$ th term is approximately $1.185$ .