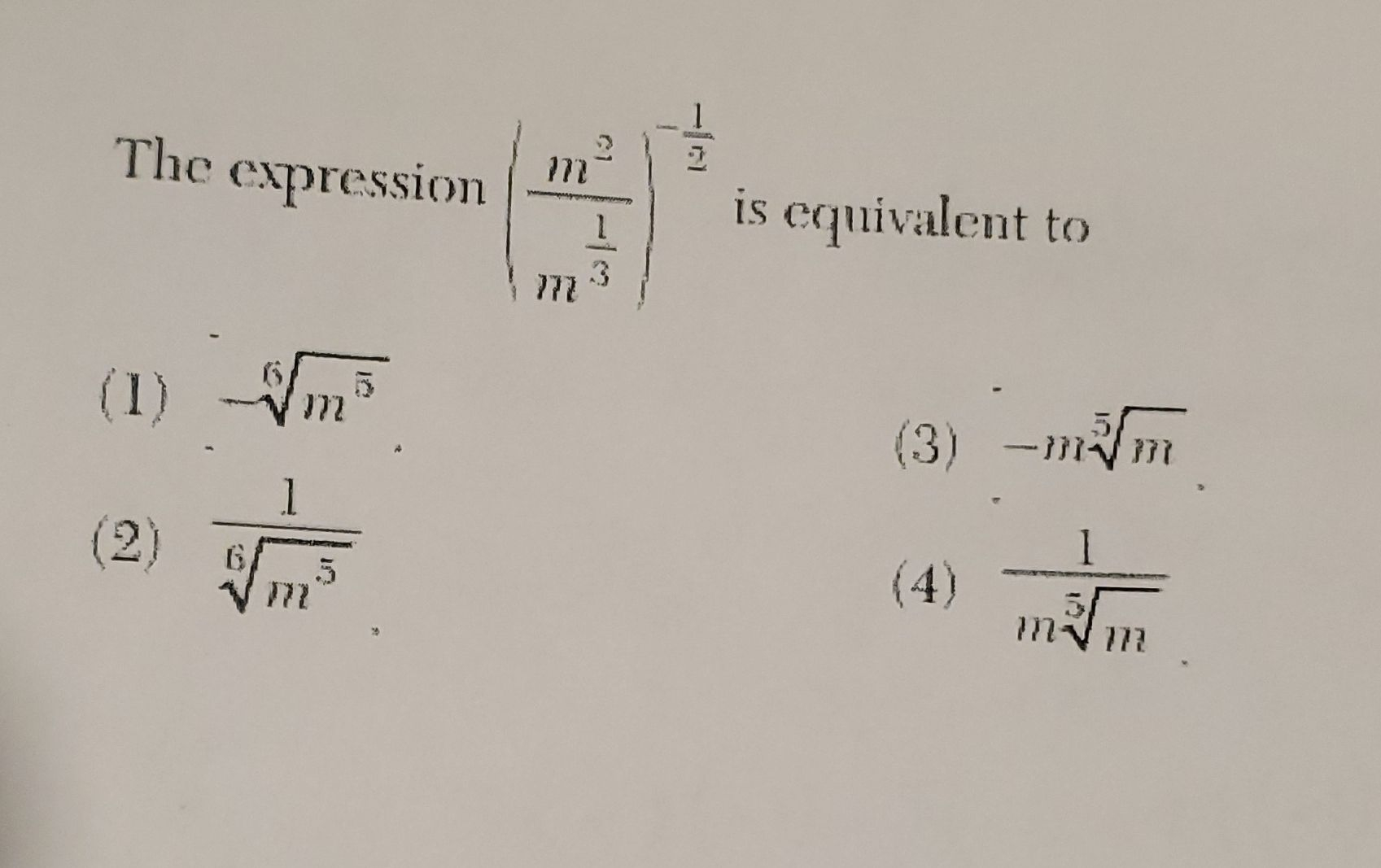AI tutor
Full solution
Q. The expression is equivalent to() () () ()
- Simplify inside parentheses: We start by simplifying the expression inside the parentheses before dealing with the outer negative exponent.The expression inside the parentheses is a quotient of powers with the same base, so we can subtract the exponents.
- Apply negative exponent: Now we apply the outer exponent of to the simplified base.
- Reciprocal of base: The negative exponent indicates that the expression is the reciprocal of the base with the positive exponent.
- Rewrite as radical expression: The expression can be rewritten as a radical expression.
- Compare with options: We compare the simplified expression with the given options.The correct option that matches our simplified expression is option .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help