The equation of an ellipse is given below. $\newline$ $\frac{x^{2}}{46}+\frac{(y+8)^{2}}{26}=1$ $\newline$ What are the foci of this ellipse? $\newline$ Choose $1$ answer: $\newline$ (A) $(0+\sqrt{20}, 8)$ and $(0-\sqrt{20}, 8)$ $\newline$ (B) $(0,8+\sqrt{20})$ and $(0,8-\sqrt{20})$ $\newline$ (C) $(0,-8+\sqrt{20})$ and $(0,-8-\sqrt{20})$ $\newline$ (D) $(0+\sqrt{20},-8)$ and $(0-\sqrt{20},-8)$

View step-by-step help

Home

Math Problems

Algebra 2

Write equations of ellipses in standard form using properties

Full solution

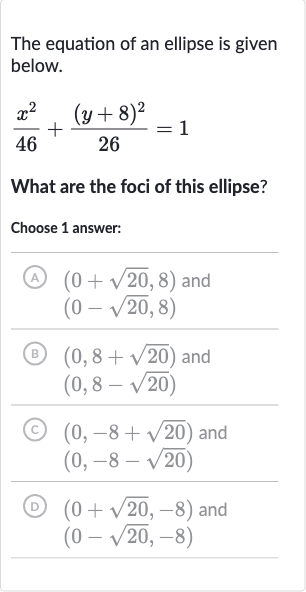
Q. The equation of an ellipse is given below.

\newline

\frac{x^{2}}{46}+\frac{(y+8)^{2}}{26}=1

\newline

What are the foci of this ellipse?

\newline

Choose

1

answer:

\newline

(A)

(0+\sqrt{20}, 8)

and

(0-\sqrt{20}, 8)

\newline

(B)

(0,8+\sqrt{20})

and

(0,8-\sqrt{20})

\newline

(C)

(0,-8+\sqrt{20})

and

(0,-8-\sqrt{20})

\newline

(D)

(0+\sqrt{20},-8)

and

(0-\sqrt{20},-8)

Given Equation of the Ellipse: The given equation of the ellipse is $(x^2)/46 + ((y+8)^2)/26 = 1$ . To find the foci, we need to identify the major and minor axes and their lengths.
Standard Form of an Ellipse: The standard form of an ellipse is $(x-h)^2/a^2 + (y-k)^2/b^2 = 1$ for a horizontal ellipse, or $(x-h)^2/b^2 + (y-k)^2/a^2 = 1$ for a vertical ellipse, where (h, k) is the center of the ellipse, $a$ is the semi-major axis length, and $b$ is the semi-minor axis length. The larger denominator corresponds to the semi-major axis length squared.
Center and Axis Lengths: In the given equation, the center of the ellipse is at ( $0$ , $-8$ ) because the equation can be rewritten as $(x-0)^2/46 + (y-(-8))^2/26 = 1$ . The semi-major axis length squared is the larger denominator, which is $46$ , and the semi-minor axis length squared is the smaller denominator, which is $26$ .
Calculate Semi-Major Axis Length: Calculate the semi-major axis length $a$ by taking the square root of $46$ : $\newline$ $a = \sqrt{46}$ .
Calculate Semi-Minor Axis Length: Calculate the semi-minor axis length $b$ by taking the square root of $26$ : $\newline$ $b = \sqrt{26}$ .
Calculate Distance to Foci: The distance from the center to the foci along the major axis is given by $c$ , where $c^2 = a^2 - b^2$ . Calculate $c$ : $\newline$ $c^2 = 46 - 26$ , $\newline$ $c^2 = 20$ , $\newline$ $c = \sqrt{20}$ .
Orientation and Foci Coordinates: Since the larger denominator is under the $x^2$ term, the major axis is horizontal, and the foci will be to the left and right of the center along the x-axis. The coordinates of the foci are therefore $(h \pm c, k)$ , where (h, k) is the center of the ellipse.
Substitute Values for Foci Coordinates: Substitute the values of $h$ , $k$ , and $c$ into the foci coordinates: $\newline$ $h = 0$ , $k = -8$ , $c = \sqrt{20}$ , $\newline$ Foci: $(0 \pm \sqrt{20}, -8)$ .
Foci of the Ellipse: The foci of the ellipse are $(0 + \sqrt{20}, -8)$ and $(0 - \sqrt{20}, -8)$ , which corresponds to answer choice (D).