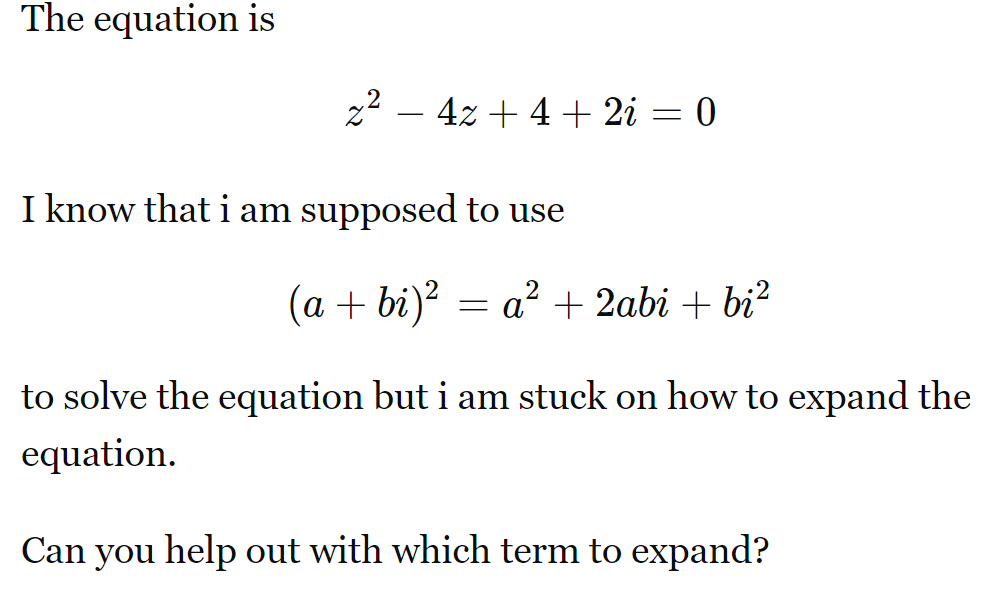The equation is z^(2)-4z+4+2i=0 I know that i am supposed to use (a+bi)^(2)=a^(2)+2abi+bi^(2) to solve the equation but i am stuck on how to expand the equation. Can you help out with which term to expand?

Question

The equation is  z^(2)-4z+4+2i=0 I know that i am supposed to use  (a+bi)^(2)=a^(2)+2abi+bi^(2) to solve the equation but i am stuck on how to expand the equation. Can you help out with which term to expand?

Bytelearn · Accepted Answer

Factor the Quadratic: We are given the quadratic equation in the complex number z: z^(2) - 4z + 4 + 2i = 0. To solve for z, we can try to factor the equation or use the quadratic formula. First, let's see if the equation can be factored. We notice that the real part of the quadratic, z^(2) - 4z + 4, is a perfect square trinomial, which factors into (z - 2)^2. We can write the equation as (z - 2)^2 + 2i = 0.Set Real and Imaginary Parts Equal: Now, we can set the real part equal to the negative of the imaginary part to find the value of z. This gives us (z - 2)^2 = -2i. We need to take the square root of both sides to solve for z. The square root of -2i can be found by expressing -2i in terms of its polar form and then taking the square root.Express -2i in Polar Form: To find the square root of -2i, we first express -2i in polar form. The magnitude of -2i is 2, and the angle (argument) is -π/2 because the point lies on the negative imaginary axis in the complex plane. Therefore, in polar form, -2i is represented as 2e^(-iπ/2).Find Square Root of -2i: The square root of 2e^(-iπ/2) is √2e^(-iπ/4), because when we take the square root of a complex number in polar form, we take the square root of the magnitude and halve the angle. Therefore, the square roots of -2i are √2e^(-iπ/4) and √2e^((3iπ)/4), since adding π to the angle gives us the other square root in the complex plane.Convert Polar Form to Rectangular Form: Now we can write the two possible values for z - 2 as z - 2 = √2e^(-iπ/4) and z - 2 = √2e^((3iπ)/4). To find the values of z, we add 2 to both sides of each equation. This gives us z = 2 + √2e^(-iπ/4) and z = 2 + √2e^((3iπ)/4).Final Solutions: We can convert the polar forms back to rectangular form (a + bi) to get the final answers. For √2e^(-iπ/4), the rectangular form is (√2/√2) + (i√2/√2) = 1 + i. For √2e^((3iπ)/4), the rectangular form is (-√2/√2) + (i√2/√2) = -1 + i. Therefore, the solutions for z are z = 2 + (1 + i) and z = 2 + (-1 + i).Simplifying the expressions for z, we get z = 3 + i and z = 1 + i as the roots of the equation z^(2) - 4z + 4 + 2i = 0.

The equation is $\newline$ $z^{2}-4 z+4+2 i=0$ $\newline$ I know that i am supposed to use $\newline$ $(a+b i)^{2}=a^{2}+2 a b i+b i^{2}$ $\newline$ to solve the equation but i am stuck on how to expand the equation. $\newline$ Can you help out with which term to expand?

Full solution

More problems from Find derivatives of using multiple formulae

Related topics