AI tutor
Full solution
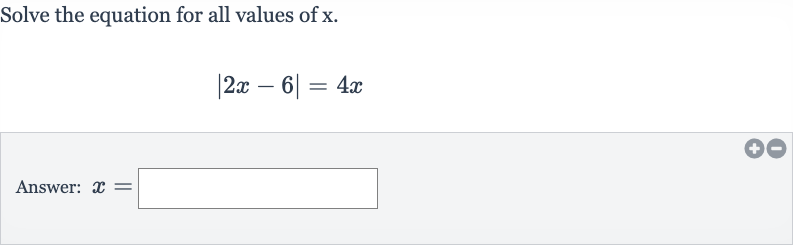
Q. Solve the equation for all values of .Answer:
- Absolute Value Equation Split: We have the equation . The absolute value equation can be split into two separate equations, one for the positive case and one for the negative case.For the positive case, we have .Now, let's solve for .Subtract from both sides to get .Divide both sides by to isolate .
- Positive Case Solution: For the negative case, we have .First, distribute the negative sign inside the parentheses.Now, let's solve for .Add to both sides to get .Divide both sides by to isolate .
- Negative Case Solution: We need to check if the solutions satisfy the original equation because when dealing with absolute values, extraneous solutions can occur.First, let's check .Substitute into the original equation .This means is not a solution.
- Check Solution - : Now, let's check .Substitute into the original equation .This means is a solution.
More problems from Evaluate absolute value expressions
QuestionGet tutor help
QuestionGet tutor help