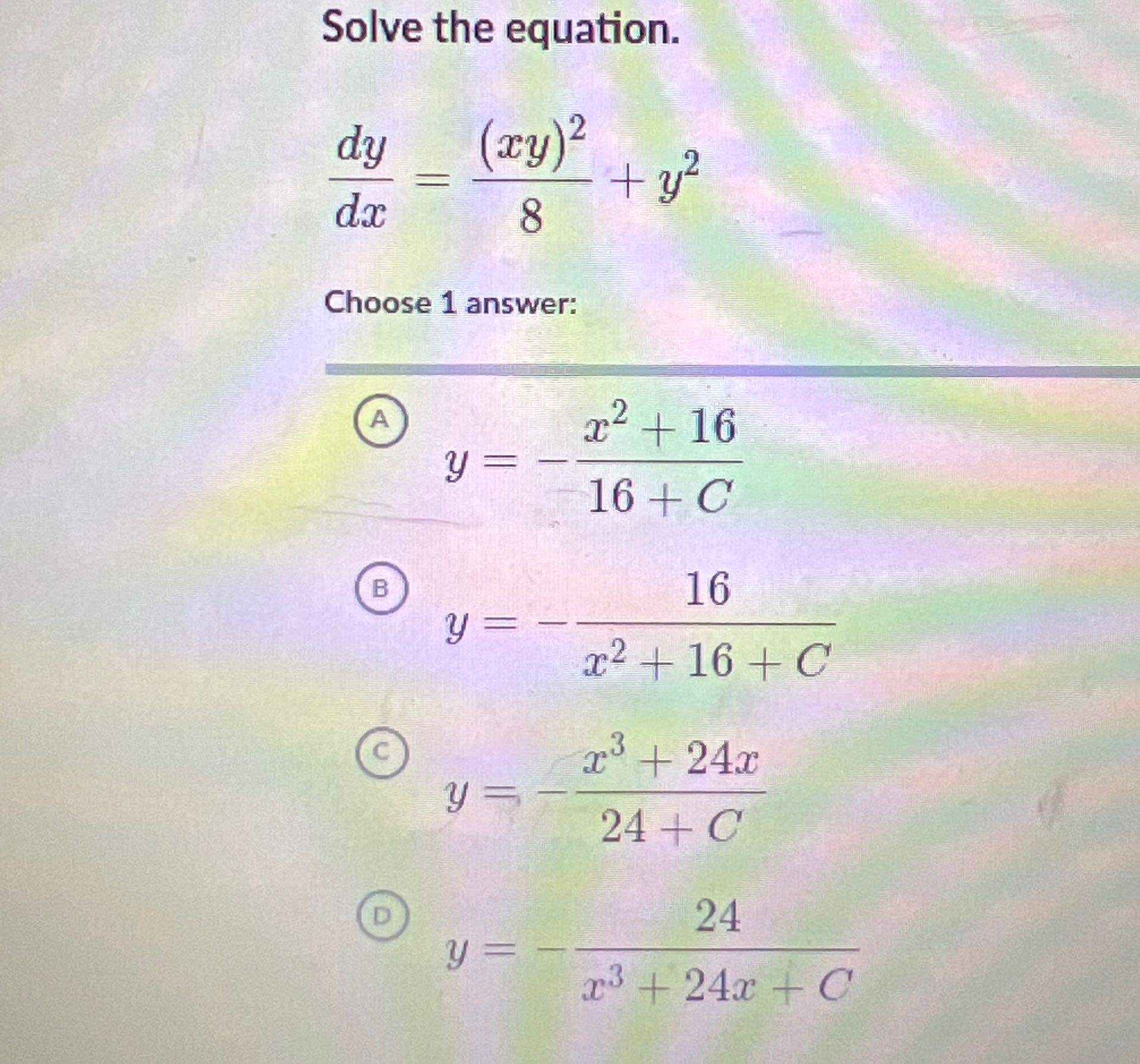AI tutor
Full solution
Q. Solve the equation.Choose answer:(A) (B) (c) (D)
- Recognize type of DE: Recognize the type of differential equation.This is a first-order non-linear differential equation.
- Attempt separation of variables: Attempt separation of variables.Assuming , divide both sides by :