AI tutor
Full solution
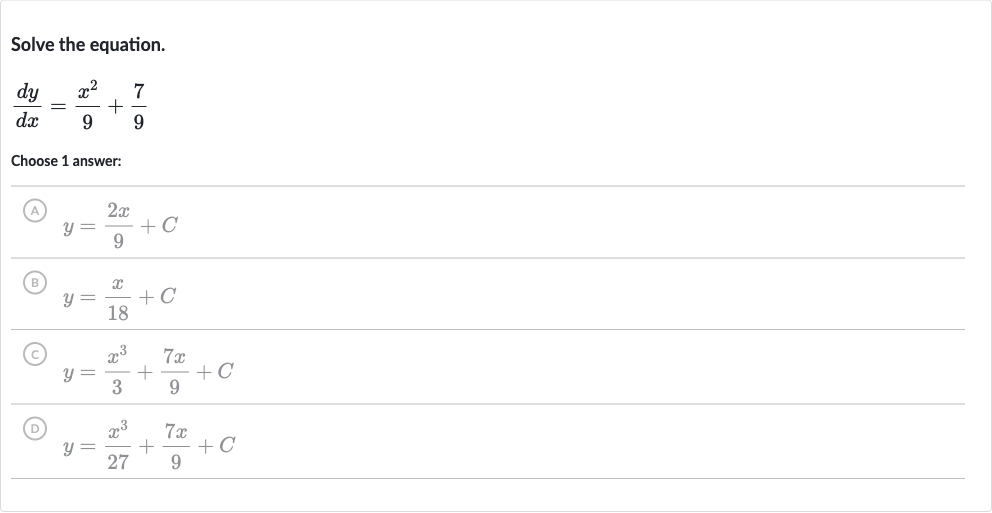
Q. Solve the equation.Choose answer:(A) (B) (C) (D)
- Integrate with respect to : Integrate both sides of the equation with respect to .
- Calculate integral of : Calculate the integral of .
- Calculate integral of : Calculate the integral of .
- Combine and add constant: Combine the results and add the constant of integration .