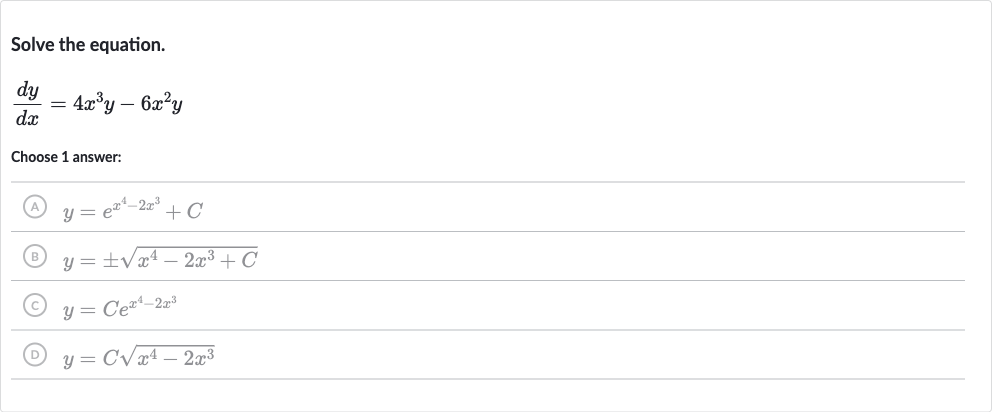
Solve the equation. (dy)/(dx)=4x^(3)y-6x^(2)y Choose 1 answer: (A) y=e^(x^(4)-2x^(3))+C (B) y=+-sqrt(x^(4)-2x^(3)+C) (C) y=Ce^(x^(4)-2x^(3)) (D) y=Csqrt(x^(4)-2)x^(3)

Question

Solve the equation.  (dy)/(dx)=4x^(3)y-6x^(2)y Choose 1 answer: (A)  y=e^(x^(4)-2x^(3))+C (B)  y=+-sqrt(x^(4)-2x^(3)+C) (C)  y=Ce^(x^(4)-2x^(3)) (D)  y=Csqrt(x^(4)-2)x^(3)

Bytelearn · Accepted Answer

Identify Equation Type: This is a first-order linear homogeneous differential equation. We can solve it by separating variables or by recognizing it as a separable differential equation. We will use the separation of variables method.Separate Variables: First, we separate the variables y and x by dividing both sides of the equation by y and by 4x^3 - 6x^2. (dy)/(y) = (4x^3 - 6x^2)dx/(4x^3 - 6x^2)Simplify Right Side: We simplify the right side of the equation by factoring out 2x^2 from both terms. (dy)/(y) = (2x^2(2x - 3))dx/(2x^2(2x - 3))Integrate Both Sides: After canceling out the common terms, we get: (dy)/(y) = dxExponentiate to Solve: Now we integrate both sides of the equation. The integral of 1/y dy is ln|y|, and the integral of dx is x. ∫(1/y) dy = ∫dx ln|y| = x + CCheck Answer Choices: To solve for y, we exponentiate both sides of the equation to get rid of the natural logarithm. e^(ln|y|) = e^(x + C) |y| = e^x * e^CSince e^C is just a constant, we can denote it as C', and since y can be positive or negative, we can drop the absolute value and include the constant C' to account for the sign. y = C'e^xWe now look at the answer choices to see which one matches our solution. (A) y=e^(x^(4)-2x^(3))+C is not correct because it does not match the form of our solution. (B) y=+-sqrt(x^(4)-2x^(3)+C) is not correct because it involves a square root and our solution does not. (C) y=Ce^(x^(4)-2x^(3)) is not correct because the exponent does not match our solution. (D) y=Csqrt(x^(4)-2)x^(3) is not correct because it involves a square root and multiplication by x^3, which does not match our solution.None of the provided answer choices match our solution y = C'e^x. It seems there might be a mistake in the separation of variables step or in the provided answer choices.

Solve the equation. $\newline$ $\frac{d y}{d x}=4 x^{3} y-6 x^{2} y$ $\newline$ Choose $1$ answer: $\newline$ (A) $y=e^{x^{4}-2 x^{3}}+C$ $\newline$ (B) $y= \pm \sqrt{x^{4}-2 x^{3}+C}$ $\newline$ (C) $y=C e^{x^{4}-2 x^{3}}$ $\newline$ (D) $y=C \sqrt{x^{4}-2} x^{3}$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics