AI tutor
Full solution
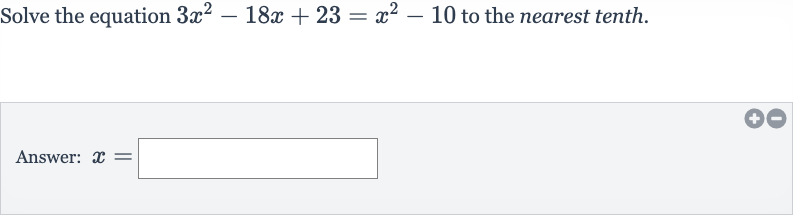
Q. Solve the equation to the nearest tenth.Answer:
- Combine and Rearrange Terms: First, we need to combine like terms and move all terms to one side of the equation to set it equal to zero.Subtract from both sides and add to both sides to get:
- Combine Like Terms: Now, combine like terms.
- Solve Quadratic Equation: Next, we need to solve the quadratic equation . We can use the quadratic formula, , where , , and . First, calculate the discriminant ():
- Calculate Discriminant: Now, plug the values into the quadratic formula:
- Apply Quadratic Formula: Simplify the square root and the fraction:We will have two solutions for :
- Calculate Solutions: Calculate the two possible values for : (to the nearest tenth) (to the nearest tenth)
More problems from Solve linear equations: mixed review
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help