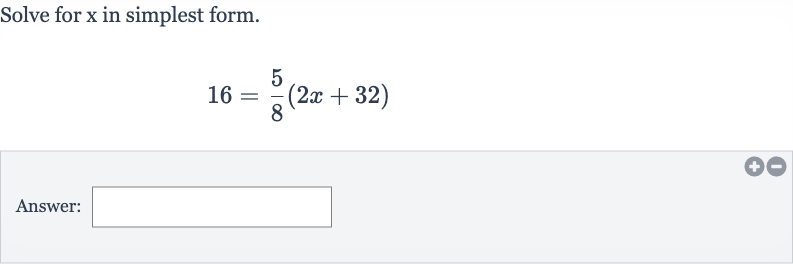AI tutor
Full solution
Q. Solve for in simplest form.Answer:
- Isolate variable term: Isolate the term with the variable . To do this, we need to get rid of the fraction by multiplying both sides of the equation by its reciprocal, which is .
- Multiply by reciprocal: Perform the multiplication on the left side of the equation.
- Perform left side multiplication: Simplify the right side of the equation. simplifies to because and cancel each other out.
- Simplify right side: Subtract from both sides to isolate the term with .
- Subtract : Convert to a fraction with the same denominator as to perform the subtraction.
- Convert to fraction: Perform the subtraction on the left side of the equation.
- Perform left side subtraction: Divide both sides by to solve for .
- Divide by : Simplify the division to find the value of .
More problems from Solve multi-step linear equations
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help