AI tutor
Full solution
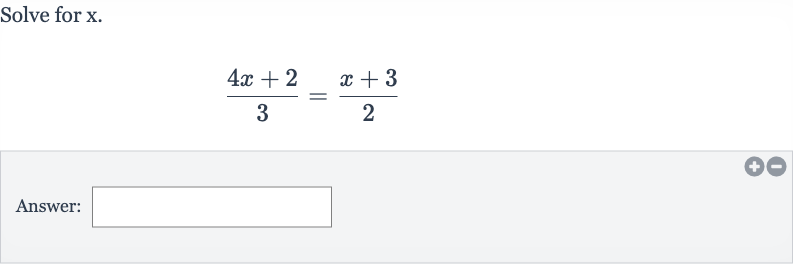
Q. Solve for .Answer:
- Identify Equation: Identify the equation to solve for . We have the equation . We need to find the value of that makes this equation true.
- Cross-Multiply: Cross-multiply to eliminate the fractions.To get rid of the fractions, we can cross-multiply. This means we multiply both sides of the equation by the denominators of the other side.
- Distribute Multiplication: Distribute the multiplication over addition on both sides.Now we distribute the multiplication over addition on both sides of the equation.
- Move Terms: Move all terms to one side and constant terms to the other side.We want to isolate on one side of the equation. To do this, we subtract from both sides and subtract from both sides.
- Divide Coefficient: Divide both sides by the coefficient of to solve for . To isolate , we divide both sides of the equation by .
More problems from Negative Exponents
QuestionGet tutor help