Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Solve for x : 10=2x-(-6x-2) Answer: x=

Solve for x x :\newline10=2x−(−6x−2) 10=2 x-(-6 x-2) \newlineAnswer: x= x=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Solve linear equations: mixed reviewright chevron icon

Full solution

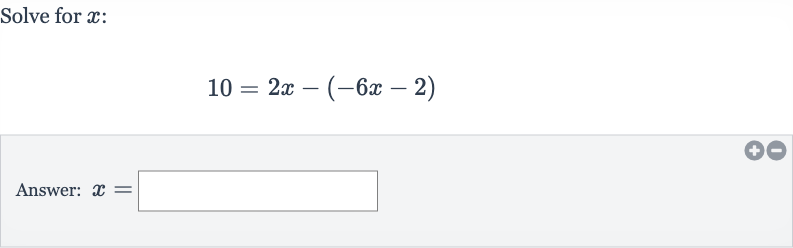
Q. Solve for x x :\newline10=2x−(−6x−2) 10=2 x-(-6 x-2) \newlineAnswer: x= x=
  1. Remove Parentheses: Simplify the equation by removing the parentheses.\newline10=2x−(−6x−2)10 = 2x - (-6x - 2)\newline10=2x+6x+210 = 2x + 6x + 2
  2. Combine Like Terms: Combine like terms on the right side of the equation.\newline10=(2x+6x)+210 = (2x + 6x) + 2\newline10=8x+210 = 8x + 2
  3. Isolate Variable Term: Isolate the variable term by subtracting 22 from both sides of the equation.\newline10−2=8x+2−210 - 2 = 8x + 2 - 2\newline8=8x8 = 8x
  4. Divide to Solve: Divide both sides by 88 to solve for xx.88=8x8\frac{8}{8} = \frac{8x}{8}1=x1 = x

More problems from Solve linear equations: mixed review

Question
Solve for x. \newline(34)x=12(\frac{3}{4})x= 12 \newlinex=x = ______
Get tutor helpright-arrow

Posted 1 year ago

Question
Solve for x. \newline−59x=15-\frac{5}{9}x= 15 \newlinex=x = ______
Get tutor helpright-arrow

Posted 1 year ago

Question
How many solutions does the following equation have?\newline5x+8−7x=−4x+15x+8-7x=-4x+1\newlineChoose 11 answer:\newline(A) No solutions\newline(B) Exactly one solution\newline(C) Infinitely many solutions
Get tutor helpright-arrow

Posted 1 year ago

Question
How many solutions does the following equation have?\newline−2z+10+7z=16z+7-2z+10+7z=16z+7\newlineChoose 11 answer:\newline(A) No solutions\newline(B) Exactly one solution\newline(C) Infinitely many solutions
Get tutor helpright-arrow

Posted 10 months ago

Question
How many solutions does the following equation have?\newline7(y−8)=7y+427(y-8)=7y+42\newlineChoose 11 answer:\newline(A) No solutions\newline(B) Exactly one solution\newline(C) Infinitely many solutions
Get tutor helpright-arrow

Posted 1 year ago

Question
How many solutions does the following equation have?\newline−9(x+6)=−9x+108-9(x+6)=-9x+108\newlineChoose 11 answer:\newline(A) No solutions\newline(B) Exactly one solution\newline(C) Infinitely many solutions
Get tutor helpright-arrow

Posted 1 year ago

Question
How many solutions does the following equation have?\newline−6(x+7)=−4x−2-6(x+7)=-4x-2\newlineChoose 11 answer:\newline(A) No solutions\newline(B) Exactly one solution\newline(C) Infinitely many solutions
Get tutor helpright-arrow

Posted 1 year ago

Question
How many solutions does the following equation have?\newline−4x−7+10x=−7+6x-4x-7+10x=-7+6x\newlineChoose 11 answer:\newline(A) No solutions\newline(B) Exactly one solution\newline(C) Infinitely many solutions
Get tutor helpright-arrow

Posted 1 year ago

Question
How many solutions does the following equation have?\newline−17(y−2)=−17y+64-17(y-2)=-17y+64\newlineChoose 11 answer:\newline(A) No solutions\newline(B) Exactly one solution\newline(C) Infinitely many solutions
Get tutor helpright-arrow

Posted 1 year ago

Question
How many solutions does the following equation have?\newline9z−6+7z=16z−69z-6+7z=16z-6\newlineChoose 11 answer:\newline(A) No solutions\newline(B) Exactly one solution\newline(C) Infinitely many solutions
Get tutor helpright-arrow

Posted 1 year ago

View all (270)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant