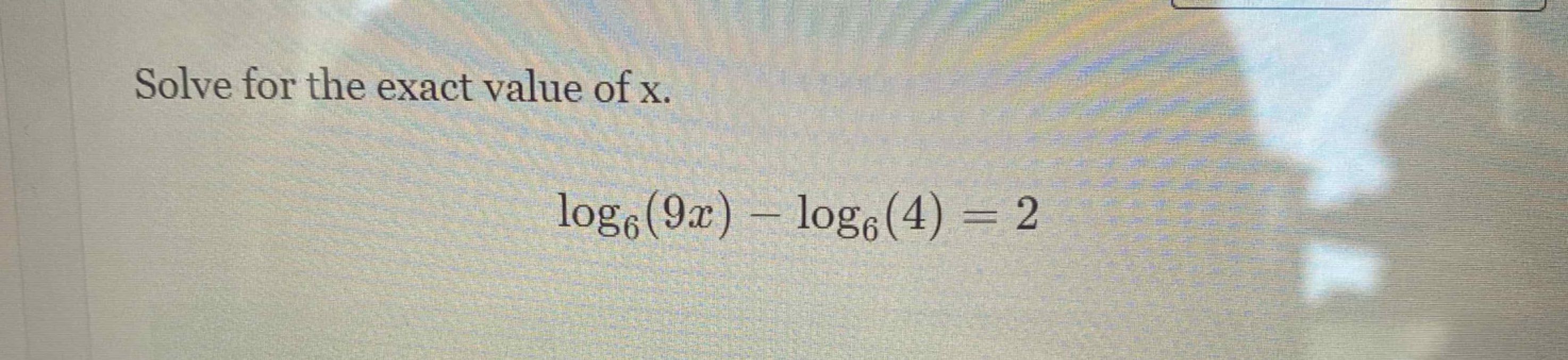Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Solve for the exact value of
x.

log_(6)(9x)-log_(6)(4)=2

Solve for the exact value of $\newline$ $x$ . $\newline$ $\log_{6}(9x)-\log_{6}(4)=2$

View step-by-step help

View step-by-step help

Find derivatives of logarithmic functions

Full solution

Q. Solve for the exact value of

\newline

x

.

\newline

\log_{6}(9x)-\log_{6}(4)=2

Use Quotient Rule: Step $1$ : Use the quotient rule for logarithms to combine the logs. $\newline$ $\log_6\left(\frac{9x}{4}\right) = 2$
Convert to Exponential Form: Step $2$ : Convert the logarithmic equation to its exponential form. $\newline$ $6^2 = \frac{9x}{4}$
Solve for x: Step $3$ : Solve for x. $\newline$ $36 = \frac{9x}{4}$ $\newline$ $144 = 9x$ $\newline$ $x = \frac{144}{9}$ $\newline$ $x = 16$

More problems from Find derivatives of logarithmic functions

Question

\lim_{\theta \rightarrow \frac{\pi}{2}} \tan ^{2}(\theta)[1-\sin (\theta)]

\newline

1

\newline

0

\newline

\frac{1}{2}

\newline

-2

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{\theta \rightarrow \frac{\pi}{2}} \frac{\sin ^{2}(2 \theta)}{1-\sin ^{2}(\theta)}

\newline

1

\newline

1

\newline

2

\newline

4

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{x \rightarrow 3} \frac{x-3}{\sqrt{4 x+4}-4}

\newline

1

\newline

-4

\newline

1

\newline

2

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{x \rightarrow-4} \frac{7 x+28}{x^{2}+x-12}

\newline

1

\newline

1

\newline

7

\newline

-1

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{x \rightarrow-3} \frac{x+3}{4-\sqrt{2 x+22}}

\newline

1

\newline

-3

\newline

-4

\newline

-\frac{3}{4}

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{x \rightarrow 1} \frac{\sqrt{5 x+4}-3}{x-1}

\newline

1

\newline

\frac{3}{5}

\newline

\frac{5}{6}

\newline

1

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{x \rightarrow-2} \frac{x^{3}+3 x^{2}+2 x}{x+2}

\newline

1

\newline

6

\newline

0

\newline

2

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{x \rightarrow \frac{\pi}{2}} \frac{\cot ^{2}(x)}{1-\sin (x)}

\newline

1

\newline

-1

\newline

-\frac{\pi}{2}

\newline

2

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{x \rightarrow \frac{\pi}{2}} \frac{\sin (2 x)}{\cos (x)}

\newline

1

\newline

\frac{1}{2}

\newline

1

\newline

2

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{\theta \rightarrow \frac{\pi}{4}} \frac{\cos (2 \theta)}{\sqrt{2} \cos (\theta)-1}

\newline

1

\newline

2

\newline

\frac{1}{2}

\newline

\sqrt{2}

\newline

(D) The limit doesn't exist

Posted 3 months ago