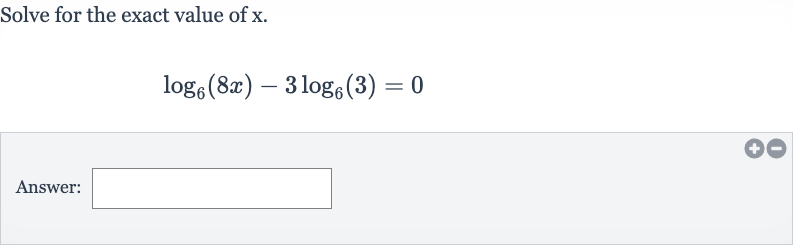
Solve for the exact value of x. log_(6)(8x)-3log_(6)(3)=0 Answer:

Question

Solve for the exact value of  x.  log_(6)(8x)-3log_(6)(3)=0 Answer:

Bytelearn · Accepted Answer

Apply Power Rule: Apply the power rule of logarithms to simplify the equation. The power rule states that a*log_b(c) = log_b(c^a), where a is a constant, b is the base of the logarithm, and c is the argument of the logarithm. We can apply this rule to the term 3log_(6)(3) to simplify the equation. log_(6)(8x) - log_(6)(3^3) = 0 log_(6)(8x) - log_(6)(27) = 0Combine Logarithmic Terms: Combine the logarithmic terms using the quotient rule. The quotient rule states that log_b(m) - log_b(n) = log_b(m/n), where b is the base of the logarithm, m and n are the arguments of the logarithm. We can combine the two logarithmic terms into a single logarithm. log_(6)(8x/27) = 0Convert to Exponential: Convert the logarithmic equation to an exponential equation. The definition of a logarithm states that if log_b(m) = n, then b^n = m. We can use this definition to convert the logarithmic equation into an exponential equation. 6^0 = 8x/27Solve for x: Solve for x. Since 6^0 = 1, we can multiply both sides of the equation by 27 to solve for x. 1 = 8x/27 27 = 8x x = 27/8

Solve for the exact value of $x$ . $\newline$ $\log _{6}(8 x)-3 \log _{6}(3)=0$ $\newline$ Answer:

Full solution

More problems from Find derivatives of logarithmic functions

Related topics

Solve for the exact value of x x x.\newlinelog⁡6(8x)−3log⁡6(3)=0 \log _{6}(8 x)-3 \log _{6}(3)=0 log6​(8x)−3log6​(3)=0\newlineAnswer:

Solve for the exact value of $x$ . $\newline$ $\log _{6}(8 x)-3 \log _{6}(3)=0$ $\newline$ Answer: