Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Solve for the exact value of x. log_(4)(6x)+2log_(4)(9)=1 Answer:

Solve for the exact value of x x .\newlinelog⁡4(6x)+2log⁡4(9)=1 \log _{4}(6 x)+2 \log _{4}(9)=1 \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find derivatives of logarithmic functionsright chevron icon

Full solution

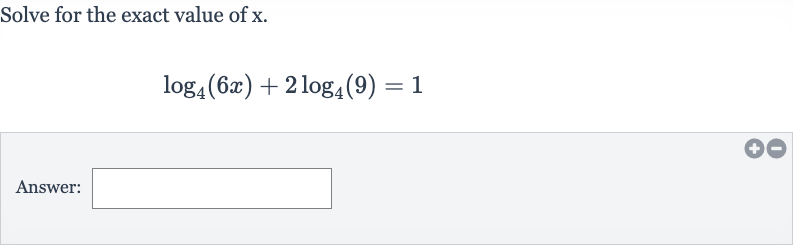
Q. Solve for the exact value of x x .\newlinelog⁡4(6x)+2log⁡4(9)=1 \log _{4}(6 x)+2 \log _{4}(9)=1 \newlineAnswer:
  1. Understand Properties of Logarithms: Understand the properties of logarithms that can be used to simplify the equation.\newlineWe can use the power rule of logarithms, which states that log⁡b(ac)=c⋅log⁡b(a)\log_b(a^c) = c\cdot\log_b(a), to simplify the second term of the equation.
  2. Apply Power Rule: Apply the power rule to the second term of the equation.\newline2log⁡4(9)2\log_{4}(9) becomes log⁡4(92)\log_{4}(9^2) because we can move the coefficient 22 as an exponent inside the logarithm.
  3. Simplify Second Term: Simplify the second term using the power rule. log⁡4(92)\log_{4}(9^2) simplifies to log⁡4(81)\log_{4}(81) because 929^2 equals 8181.
  4. Rewrite Equation: Rewrite the original equation using the simplified second term.\newlineThe equation now is log⁡4(6x)+log⁡4(81)=1\log_{4}(6x) + \log_{4}(81) = 1.
  5. Combine Logarithmic Terms: Combine the logarithmic terms on the left side using the product rule of logarithms.\newlineThe product rule states that log⁡b(m)+log⁡b(n)=log⁡b(m∗n)\log_b(m) + \log_b(n) = \log_b(m*n), so we can combine the two logarithmic terms into a single logarithm.
  6. Apply Product Rule: Apply the product rule to combine the logarithmic terms. log⁡4(6x)+log⁡4(81)\log_{4}(6x) + \log_{4}(81) becomes log⁡4(6x⋅81)\log_{4}(6x \cdot 81).
  7. Simplify Expression: Simplify the expression inside the logarithm. 6x×816x\times 81 simplifies to 486x486x because 66 times 8181 equals 486486.
  8. Rewrite with Combined Logarithm: Rewrite the equation with the combined logarithm.\newlineThe equation now is log⁡4(486x)=1\log_{4}(486x) = 1.
  9. Convert to Exponential Equation: Convert the logarithmic equation to an exponential equation.\newlineUsing the definition of a logarithm, log⁡b(a)=c\log_b(a) = c can be rewritten as bc=ab^c = a, we can find the value of xx.
  10. Apply Definition of Logarithm: Apply the definition of a logarithm to solve for xx.41=486x4^1 = 486x, because log⁡4(486x)=1\log_{4}(486x) = 1 means that 44 raised to the power of 11 equals 486x486x.
  11. Solve for x: Solve for x.\newlineDivide both sides by 486486 to isolate xx.\newlinex=4486x = \frac{4}{486}
  12. Simplify Fraction: Simplify the fraction to find the exact value of xx.4486\frac{4}{486} can be simplified by dividing both numerator and denominator by 22.x=2243x = \frac{2}{243}

More problems from Find derivatives of logarithmic functions

Question
Find the derivative of f(x) f(x) .\newlinef(x)=cos⁡(x) f(x) = \cos(x) \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 7 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=tan⁡(x) f(x) = \tan(x) \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=ex f(x) = e^x \newlinef′(x)= f'\left(x\right) = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=ln⁡(x) f(x) = \ln(x) \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=tan⁡−1x f(x) = \tan^{-1}{x} \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=xex f(x) = x e^x \newlinef′(x)= f'\left(x\right) = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
Find the derivative of f(x) f(x) . \newlinef(x)=exx f(x) = \frac{e^x}{x} \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
Find the derivative of f(x) f(x) . \newline f(x)=e(x+1) f(x) = e^{(x + 1)} \newline f′(x)= f'\left(x\right) = ______
Get tutor helpright-arrow

Posted 7 months ago

Question
Find the derivative of f(x) f(x) . \newlinef(x)=x+3 f(x) = \sqrt{x+3} \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
Find the derivative of g(x) g(x). \newline g(x)=ln⁡(2x) g(x) = \ln(2x) \newline g′(x)= g^{\prime}(x) = ______
Get tutor helpright-arrow

Posted 9 months ago

View all (111)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant