AI tutor
Full solution
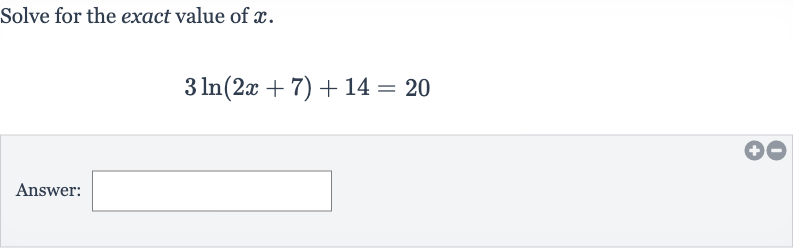
Q. Solve for the exact value of .Answer:
- Isolate natural logarithm term: First, we need to isolate the natural logarithm term by subtracting from both sides of the equation.
- Simplify by subtraction: Now, we simplify the equation by performing the subtraction.
- Divide to isolate logarithm: Next, we divide both sides of the equation by to isolate the natural logarithm.
- Get logarithm by itself: After dividing, we get the natural logarithm by itself.
- Exponentiate using base e: To eliminate the natural logarithm, we will exponentiate both sides of the equation using the base e.
- Simplify left side: Since for any , we can simplify the left side of the equation.
- Isolate term with x: Now, we subtract from both sides to isolate the term with .
- Simplify by subtraction: Simplify the equation by performing the subtraction.
- Divide to solve for x: Finally, we divide both sides by to solve for .
- Get exact value of x: After dividing, we get the exact value of x.
More problems from Solve linear equations: mixed review
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help