AI tutor
Full solution
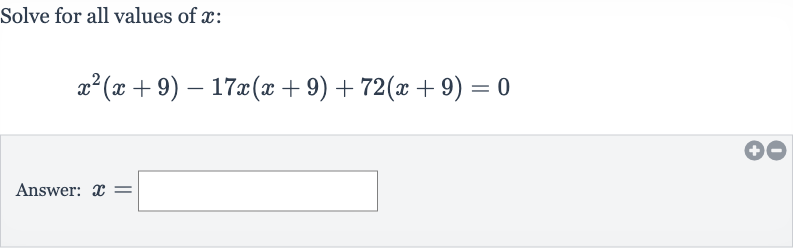
Q. Solve for all values of :Answer:
- Factor out common term: First, notice that each term has a common factor of . Factor out from the equation.
- Find x for first factor: Now, we need to find the values of that make each factor equal to zero. First, set the first factor equal to zero.
- Factor and solve quadratic equation: Next, set the second factor equal to zero and solve for .To solve this quadratic equation, we can factor it.
- Solve for x in quadratic equation: Now, set each factor of the quadratic equation equal to zero and solve for x. => =>
More problems from Solve linear equations: mixed review
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help