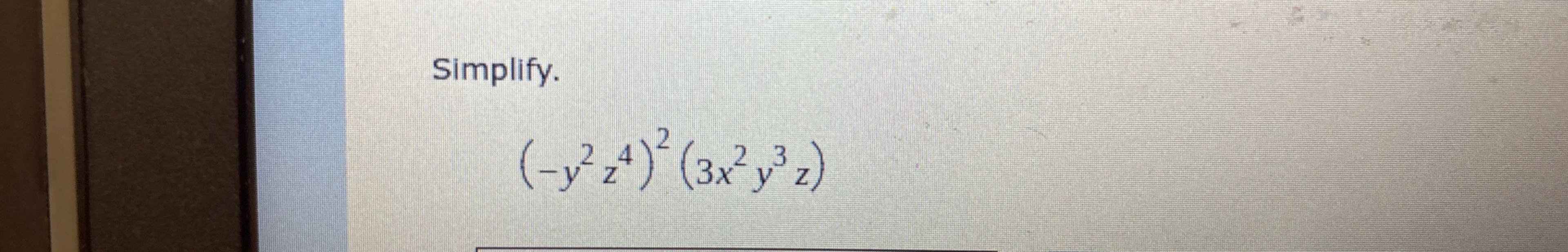AI tutor
Full solution
Q. Simplify.
- Simplify Exponents: First, let's simplify . We need to square both the and terms.So,
- Multiply Terms: Now, multiply by . We combine like terms by adding the exponents for and . And multiply the coefficients: So,
- Check for Errors: Now we check for any math errors in the previous steps.Everything looks correct, so we can conclude that the simplified form is