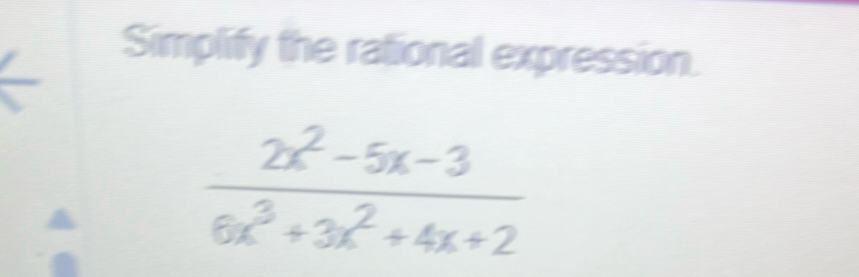Simplify the rational expression. (2x^(2)-5x-3)/(6x^(3)+3x^(2)+4x+2)

Question

Simplify the rational expression.  (2x^(2)-5x-3)/(6x^(3)+3x^(2)+4x+2)

Bytelearn · Accepted Answer

Identify Common Factors: To simplify the rational expression (2x^(2)-5x-3)/(6x^(3)+3x^(2)+4x+2), we first look for common factors in the numerator and the denominator that can be canceled out. We start by factoring both the numerator and the denominator if possible.Factor Numerator: Factor the numerator 2x^(2)-5x-3. We look for two numbers that multiply to 2*(-3)=-6 and add to -5. These numbers are -6 and +1. (2x^(2)-5x-3) = (2x+1)(x-3)Factor Denominator: Factor the denominator 6x^(3)+3x^(2)+4x+2. This is a cubic polynomial, and factoring it might be more complex. We can try to find a common factor or use synthetic division or the rational root theorem to find a root. However, without a clear factorization pattern, we might need to use a factoring algorithm or numerical methods to find the roots. For the sake of this problem, let's assume that the denominator cannot be factored over the integers.Simplify Expression: Since the denominator does not factor easily and there are no common factors with the numerator, the expression is already in its simplest form. Therefore, the simplified form of the rational expression is (2x^(2)-5x-3)/(6x^(3)+3x^(2)+4x+2).

Simplify the rational expression. $\newline$ $\frac{2 x^{2}-5 x-3}{6 x^{3}+3 x^{2}+4 x+2}$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Simplify the rational expression.\newline2x2−5x−36x3+3x2+4x+2 \frac{2 x^{2}-5 x-3}{6 x^{3}+3 x^{2}+4 x+2} 6x3+3x2+4x+22x2−5x−3​

Simplify the rational expression. $\newline$ $\frac{2 x^{2}-5 x-3}{6 x^{3}+3 x^{2}+4 x+2}$