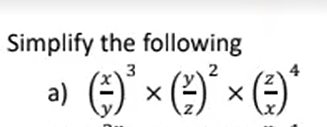Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Simplify the following a) ((x)/(y))^(3)×((y)/(z))^(2)×((z)/(x))^(4)

Simplify the following\newline(xy)3×(yz)2×(zx)4 \left(\frac{x}{y}\right)^{3} \times\left(\frac{y}{z}\right)^{2} \times\left(\frac{z}{x}\right)^{4}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 8right chevron icon
Writing from expanded to exponent formright chevron icon

Full solution

Q. Simplify the following\newline(xy)3×(yz)2×(zx)4 \left(\frac{x}{y}\right)^{3} \times\left(\frac{y}{z}\right)^{2} \times\left(\frac{z}{x}\right)^{4}
  1. Combine like terms: Combine the powers of the same bases by adding or subtracting the exponents. \newline(xy)3×(yz)2×(zx)4=x3y3×y2z2×z4x4\left(\frac{x}{y}\right)^3 \times \left(\frac{y}{z}\right)^2 \times \left(\frac{z}{x}\right)^4 = \frac{x^3}{y^3} \times \frac{y^2}{z^2} \times \frac{z^4}{x^4}
  2. Simplify exponents: Simplify by combining like terms.\newline=x3⋅y2⋅z4y3⋅z2⋅x4= \frac{x^3 \cdot y^2 \cdot z^4}{y^3 \cdot z^2 \cdot x^4}\newline=x3−4⋅y2−3⋅z4−2= x^{3-4} \cdot y^{2-3} \cdot z^{4-2}\newline=x−1⋅y−1⋅z2= x^{-1} \cdot y^{-1} \cdot z^{2}
  3. Rewrite negative exponents: Rewrite negative exponents as fractions.\newline=1x×1y×z2= \frac{1}{x} \times \frac{1}{y} \times z^{2}\newline=z2xy= \frac{z^{2}}{xy}

More problems from Writing from expanded to exponent form

Question
Write the expression using an exponent.\newline2×22 \times 2\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the expression. 4−42 4 - 4^2 ____
Get tutor helpright-arrow

Posted 2 months ago

Question
x2=4x^2 = 4
Get tutor helpright-arrow

Posted 1 month ago

Question
x2=9x^2 = 9
Get tutor helpright-arrow

Posted 3 months ago

Question
Solve for x. \newlinex2=0x^2 = 0 \newlineWrite your answer in simplified, rationalized form. \newlinex=x = _____ or x=x = _____
Get tutor helpright-arrow

Posted 3 months ago

Question
Solve for xx. \newline8=2x8 = 2^x \newline x=x = _____
Get tutor helpright-arrow

Posted 3 months ago

Question
Solve for xx. \newline6=7x6 = 7^x \newline x=x = _____
Get tutor helpright-arrow

Posted 3 months ago

Question
Select the equivalent expression.\newline((8−5)/(2−2))−4=?((8^{-5})/(2^{-2}))^{-4}=?\newlineChoose 11 answer:\newline(A) \newline(820)/(28)(8^{20})/(2^{8})\newline(B) \newline(26)/(89)(2^{6})/(8^{9})\newline(C) \newline(1)/(8⋅22)(1)/(8\cdot 2^{2})
Get tutor helpright-arrow

Posted 5 days ago

Question
Select the equivalent expression.\newline(b745)−3= ?\left(\frac{b^{7}}{4^{5}}\right)^{-3}=\,?\newlineChoose 11 answer:\newline(A) b21415\frac{b^{21}}{4^{15}}\newline(B) 415b21\frac{4^{15}}{b^{21}}\newline(C) b−21⋅4−15b^{-21}\cdot 4^{-15}
Get tutor helpright-arrow

Posted 1 month ago

Question
Select the equivalent expression.\newline(33⋅66)−3=(3^{3}\cdot6^{6})^{-3}=?\newlineChoose 11 answer:\newline(A) 139⋅618\frac{1}{3^{9}\cdot6^{18}}\newline(B) 61839\frac{6^{18}}{3^{9}}\newline(C) 39618\frac{3^{9}}{6^{18}}
Get tutor helpright-arrow

Posted 1 month ago

View all (51)