Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

$Simplify the expression. Write your answers using integers or improper fractions. -(1)/(2)v-3(-3v-(5)/(2)) Answer:$

Simplify the expression. Write your answers using integers or improper fractions. $\newline$ $-\frac{1}{2} v-3\left(-3 v-\frac{5}{2}\right)$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Powers with decimal and fractional bases

Full solution

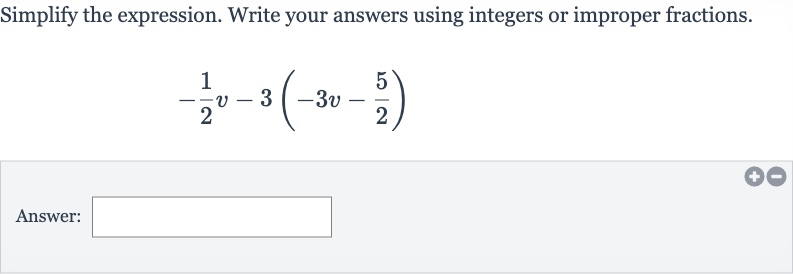
Q. Simplify the expression. Write your answers using integers or improper fractions.

\newline

-\frac{1}{2} v-3\left(-3 v-\frac{5}{2}\right)

\newline

Answer:

Distribute negative sign: Distribute the negative sign inside the parentheses. $\newline$ We have the expression $-\left(\frac{1}{2}\right)v - 3(-3v - \left(\frac{5}{2}\right))$ . First, we distribute the $-3$ across the parentheses to both $-3v$ and $-\frac{5}{2}$ . $\newline$ $-3 \times -3v = 9v$ $\newline$ $-3 \times -\left(\frac{5}{2}\right) = \frac{15}{2}$
Combine distributed terms: Combine the distributed terms with the rest of the expression. $\newline$ Now we combine the terms from the distribution with the initial $-\frac{1}{2}v$ . $\newline$ $-\frac{1}{2}v + 9v + \frac{15}{2}$
Combine like terms: Combine like terms. $\newline$ We need to combine the $v$ terms. To do this, we need a common denominator. The common denominator for $\frac{1}{2}$ and $9$ (which is $\frac{9}{1}$ ) is $2$ . $\newline$ $-\left(\frac{1}{2}\right)v$ is the same as $-\frac{1}{2}v$ . $\newline$ $9v$ is the same as $\frac{18}{2}v$ . $\newline$ Now we add $-\frac{1}{2}v$ and $\frac{18}{2}v$ . $\newline$ $\frac{1}{2}$ $1$
Write final expression: Write the final simplified expression. $\newline$ Now we have the $v$ term and the constant term. The final expression is: $\newline$ $(\frac{17}{2})v + \frac{15}{2}$

More problems from Powers with decimal and fractional bases

Question

Write the expression using an exponent.

\newline

2 \times 2

\newline

Posted 8 months ago

Question

Evaluate the expression.

4 - 4^2

Posted 8 months ago

Question

x^2 = 4

Posted 7 months ago

Question

x^2 = 9

Posted 9 months ago

Question

\newline

x^2 = 0

\newline

Write your answer in simplified, rationalized form.

\newline

x =

x =

Posted 9 months ago

Question

x

\newline

8 = 2^x

\newline

x =

Posted 9 months ago

Question

x

\newline

6 = 7^x

\newline

x =

Posted 9 months ago

Question

Select the equivalent expression.

\newline

((8^{-5})/(2^{-2}))^{-4}=?

\newline

1

\newline

\newline

(8^{20})/(2^{8})

\newline

\newline

(2^{6})/(8^{9})

\newline

\newline

(1)/(8\cdot 2^{2})

Posted 6 months ago

Question

Select the equivalent expression.

\newline

\left(\frac{b^{7}}{4^{5}}\right)^{-3}=\,?

\newline

1

\newline

\frac{b^{21}}{4^{15}}

\newline

\frac{4^{15}}{b^{21}}

\newline

b^{-21}\cdot 4^{-15}

Posted 7 months ago

Question

Select the equivalent expression.

\newline

(3^{3}\cdot6^{6})^{-3}=

\newline

1

\newline

\frac{1}{3^{9}\cdot6^{18}}

\newline

\frac{6^{18}}{3^{9}}

\newline

\frac{3^{9}}{6^{18}}

Posted 8 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant