Resources

Testimonials

Plans

Resources

Testimonials

Plans

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

$Simplify the expression. Write your answers using integers or improper fractions. (1)/(2)(-(5)/(4)f-(7)/(4))-4f Answer:$

Simplify the expression. Write your answers using integers or improper fractions. $\newline$ $\frac{1}{2}\left(-\frac{5}{4} f-\frac{7}{4}\right)-4 f$ $\newline$ Answer:

View step-by-step help

Home

Math Problems

Algebra 1

Multiplication with rational exponents

Full solution

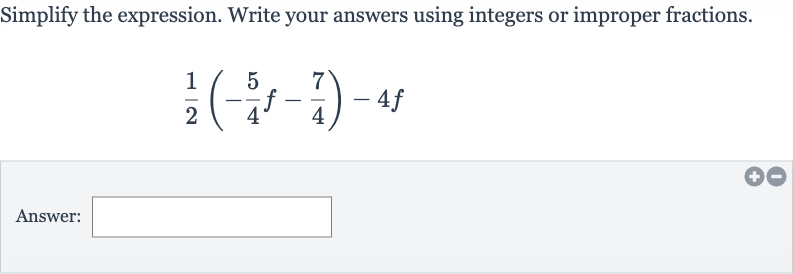
Q. Simplify the expression. Write your answers using integers or improper fractions.

\newline

\frac{1}{2}\left(-\frac{5}{4} f-\frac{7}{4}\right)-4 f

\newline

Answer:

Distribute negative sign: Distribute the negative sign inside the parentheses. $\newline$ We have the expression $(1)/(2)(-(5)/(4)f-(7)/(4))-4f$ . First, we distribute the negative sign to both terms inside the parentheses. $\newline$ $(1)/(2)(-1 \times (5)/(4)f - 1 \times (7)/(4)) - 4f$ $\newline$ = $(1)/(2)(-(5)/(4)f - (7)/(4)) - 4f$
Multiply by $(1)/(2)$ : Multiply each term inside the parentheses by $(1)/(2)$ . $\newline$ Now we multiply each term inside the parentheses by $(1)/(2)$ . $\newline$ (\(1)/( $2$ ) \times (-( $5$ )/( $4$ )f) + ( $1$ )/( $2$ ) \times (-( $7$ )/( $4$ )) - $4$ f $\newline$ = ( $1$ )/( $2$ ) \times -( $5$ )/( $4$ )f - ( $1$ )/( $2$ ) \times ( $7$ )/( $4$ ) - $4$ f
Simplify multiplication: Simplify the multiplication. $\newline$ We simplify the multiplication by reducing the fractions. $\newline$ = $\left(-\frac{5}{8}f\right) - \frac{7}{8} - 4f$
Combine like terms: Combine like terms. $\newline$ We have two terms with the variable $f$ , so we combine them. $\newline$ $= \left(-\frac{5}{8}f\right) - 4f - \frac{7}{8}$
Convert whole number: Convert the whole number to a fraction with the same denominator as the fraction term. $\newline$ To combine the terms with $f$ , we need to convert $4f$ to a fraction with a denominator of $8$ . $\newline$ $4f = 4 \times \frac{8}{8}f = \frac{32}{8}f$ $\newline$ Now we can combine the terms. $\newline$ $= \left(-\frac{5}{8}f\right) - \frac{32}{8}f - \frac{7}{8}$
Add fractions with variable: Add the fractions with the variable $f$ . $\newline$ Now we add the fractions with the variable $f$ . $\newline$ $= \left(-\frac{5}{8}f\right) - \frac{32}{8}f$ $\newline$ $= \left(-\frac{5+32}{8}\right)f$ $\newline$ = \left(-\frac{$37$}{$8$}\right)f
Write final expression: Write the final simplified expression.\(\newlineNow we write the final simplified expression by including the constant term. $\newline$ $= \frac{-(37)}{8}f - \frac{7}{8}$