AI tutor
Full solution
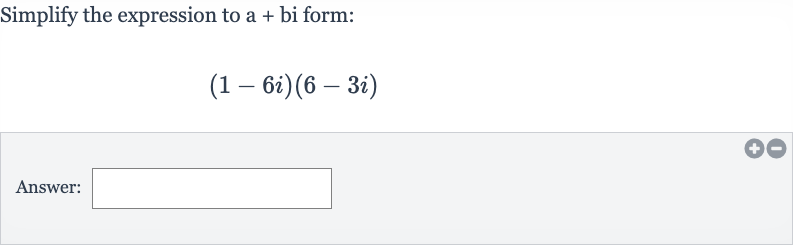
Q. Simplify the expression to a + bi form:Answer:
- Apply Distributive Property: First, we will use the distributive property (also known as the FOIL method for binomials) to multiply the two complex numbers. This involves multiplying each term in the first complex number by each term in the second complex number.
- Perform Multiplication: Now, we will perform the multiplication for each pair of terms.Remember that .
- Substitute and Combine Terms: Next, we will substitute with and combine like terms.This simplifies to:
- Combine Real and Imaginary Parts: Now, we combine the real parts and the imaginary parts.This simplifies to:
More problems from Simplify variable expressions using properties
QuestionGet tutor help