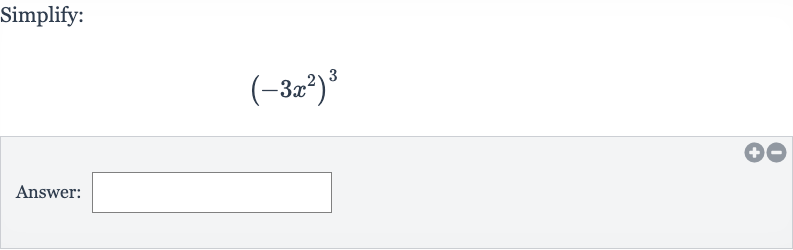AI tutor
Full solution
Q. Simplify:Answer:
- Apply Power Rule: Apply the power of a power rule, which states that a^m)^n = a^{m*n}\. In this case, we have \$\left(-3x^2\right)^3, so we need to raise both (-3\)\ and \x^\ to the power of (3\)\.
- Calculate Cubes: Calculate the cube of and the cube of separately.
- Combine Results: Combine the results from Step to get the final simplified expression.
More problems from Simplify variable expressions using properties
QuestionGet tutor help