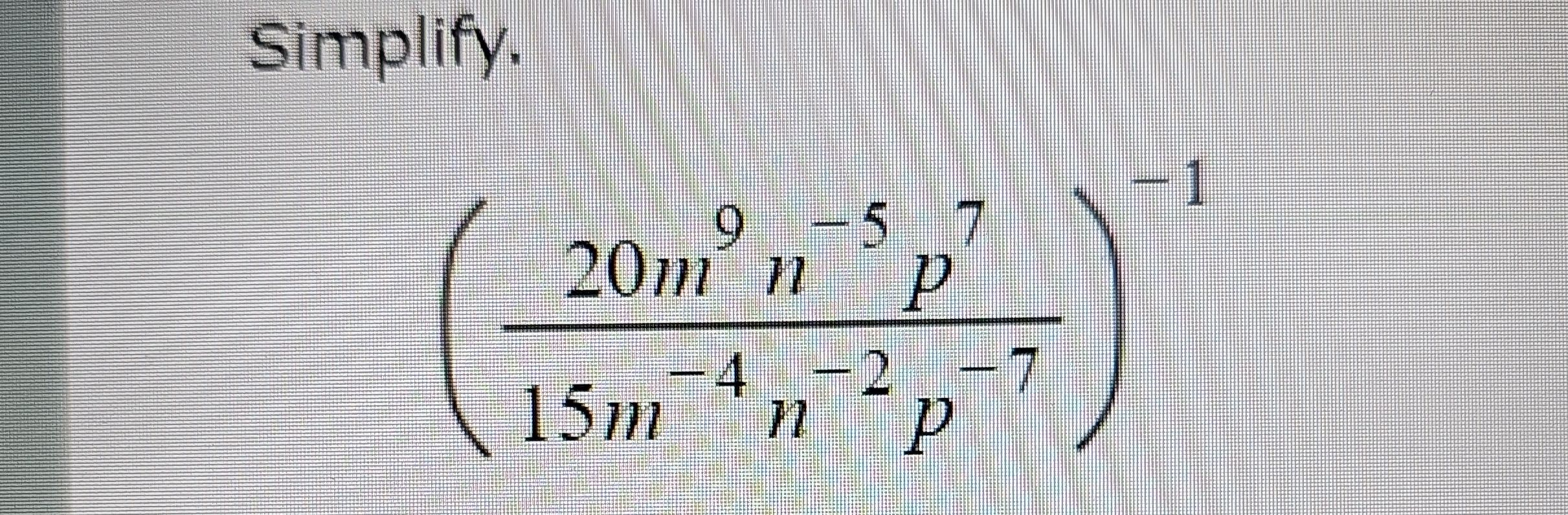Simplify. ((20m^(9)n^(-5)p^(7))/(15m^(-4)n^(-2)p^(-7)))^(-1)

Question

Simplify.  ((20m^(9)n^(-5)p^(7))/(15m^(-4)n^(-2)p^(-7)))^(-1)

Bytelearn · Accepted Answer

Evaluate Fraction Simplification: Evaluate the expression inside the parentheses by simplifying the fraction. We can simplify the fraction by dividing the coefficients and subtracting the exponents of the variables with the same base. (20/15) simplifies to (4/3) since both 20 and 15 are divisible by 5. For the variables, we use the property of exponents that states a^(m)/a^(n) = a^(m-n). So, m^(9)/m^(-4) becomes m^(9-(-4)) = m^(13). n^(-5)/n^(-2) becomes n^(-5-(-2)) = n^(-3). p^(7)/p^(-7) becomes p^(7-(-7)) = p^(14). The simplified form inside the parentheses is (4/3)m^(13)n^(-3)p^(14).Apply Negative Exponent Rule: Now, apply the negative exponent rule which states (a/b)^(-1) = b/a. We apply this rule to the entire expression (4/3)m^(13)n^(-3)p^(14). This means we take the reciprocal of the fraction and change the sign of the exponents of the variables. The reciprocal of (4/3) is (3/4). The exponents of the variables change sign, so m^(13) becomes m^(-13), n^(-3) becomes n^(3), and p^(14) becomes p^(-14). The simplified form after applying the negative exponent is (3/4)m^(-13)n^(3)p^(-14).

Simplify. $\newline$ $\left(\frac{20 m^{9} n^{-5} p^{7}}{15 m^{-4} n^{-2} p^{-7}}\right)^{-1}$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Simplify.\newline(20m9n−5p715m−4n−2p−7)−1 \left(\frac{20 m^{9} n^{-5} p^{7}}{15 m^{-4} n^{-2} p^{-7}}\right)^{-1} (15m−4n−2p−720m9n−5p7​)−1

Simplify. $\newline$ $\left(\frac{20 m^{9} n^{-5} p^{7}}{15 m^{-4} n^{-2} p^{-7}}\right)^{-1}$