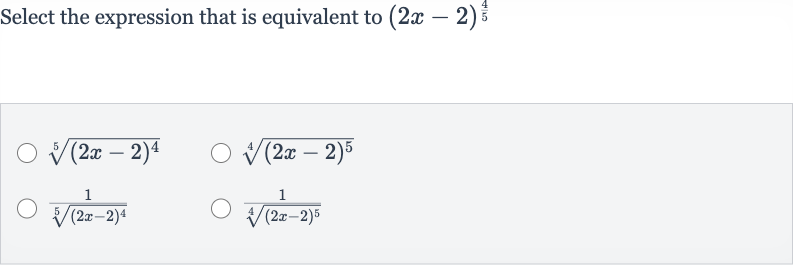Select the expression that is equivalent to (2x-2)^((4)/(5)) root(5)((2x-2)^(4)) root(4)((2x-2)^(5)) (1)/(root(5)((2x-2)^(4))) (1)/(root(4)((2x-2)^(5)))

Question

Select the expression that is equivalent to  (2x-2)^((4)/(5))  root(5)((2x-2)^(4))  root(4)((2x-2)^(5))  (1)/(root(5)((2x-2)^(4)))  (1)/(root(4)((2x-2)^(5)))

Bytelearn · Accepted Answer

Understand Notation: We need to understand the notation of the given expression. The exponent (4/5) can be interpreted as raising the base (2x-2) to the 4th power and then taking the 5th root of the result, or equivalently, taking the 5th root of the base (2x-2) and then raising it to the 4th power. This is because of the property of exponents that states (a^(m/n)) = root(n)(a^m) = (root(n)(a))^m.Analyze Options: Now let's analyze the given options one by one to see which one matches the interpretation from Step 1.  Option 1: root(5)((2x-2)^(4)) This option represents taking the 5th root of (2x-2) raised to the 4th power, which is exactly the interpretation of the original expression (2x-2)^(4/5).Option 1: Option 2: root(4)((2x-2)^(5)) This option represents taking the 4th root of (2x-2) raised to the 5th power. This does not match the original expression's exponent of (4/5).Option 2: Option 3: (1)/(root(5)((2x-2)^(4))) This option represents the reciprocal of the 5th root of (2x-2) raised to the 4th power. This is not equivalent to the original expression because it is the inverse of what we are looking for.Option 3: Option 4: (1)/(root(4)((2x-2)^(5))) This option represents the reciprocal of the 4th root of (2x-2) raised to the 5th power. Again, this is not equivalent to the original expression because it is the inverse and also does not match the (4/5) exponent.Option 4: Based on the analysis of the options, we can conclude that the expression equivalent to (2x-2)^(4/5) is root(5)((2x-2)^(4)), which is Option 1.

Select the expression that is equivalent to $(2 x-2)^{\frac{4}{5}}$ $\newline$ $\sqrt[5]{(2 x-2)^{4}}$ $\newline$ $\sqrt[4]{(2 x-2)^{5}}$ $\newline$ $\frac{1}{\sqrt[5]{(2 x-2)^{4}}}$ $\newline$ $\frac{1}{\sqrt[4]{(2 x-2)^{5}}}$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics