AI tutor
Full solution
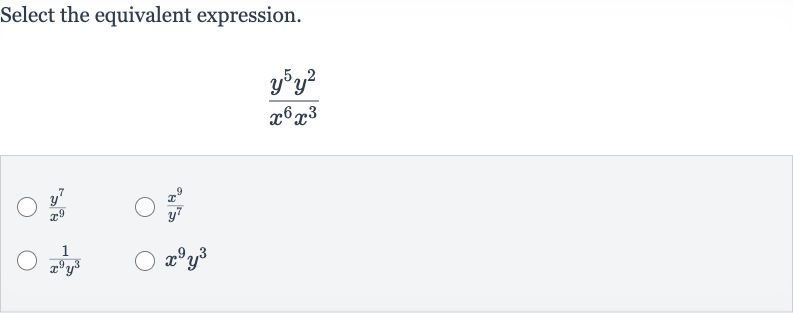
Q. Select the equivalent expression.
- Apply Exponent Properties: To find the equivalent expression, we need to simplify the given expression using the properties of exponents.
- Simplify Numerator: When multiplying powers with the same base, we add the exponents. So for the numerator , we add the exponents and .
- Simplify Denominator: Similarly, for the denominator , we add the exponents and .
- Combine Simplified Terms: Now we have the simplified form of the numerator and denominator. We can write the entire expression as:
- Identify Equivalent Expression: Comparing the simplified expression with the given options, we find that the equivalent expression is .