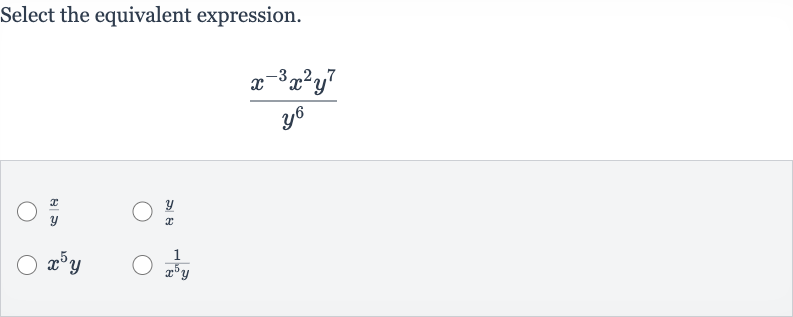AI tutor
Full solution
Q. Select the equivalent expression.
- Simplify terms: To find the equivalent expression, we need to simplify the given expression using the properties of exponents.
- Simplify terms: First, we simplify the terms by adding the exponents since they have the same base and are being multiplied.
- Combine and terms: Next, we simplify the terms by subtracting the exponents since is being divided by ..
- Final equivalent expression: Now we combine the simplified and terms.
- Final equivalent expression: Now we combine the simplified and terms..The expression is equivalent to .Therefore, the equivalent expression is .