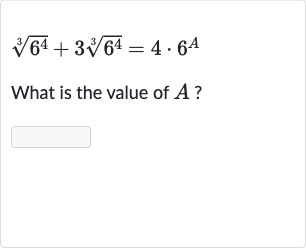
root(3)(6^(4))+3root(3)(6^(4))=4*6^(A) What is the value of A ?

Question

root(3)(6^(4))+3root(3)(6^(4))=4*6^(A) What is the value of  A ?

Bytelearn · Accepted Answer

Recognize cube root: We are given the equation: root(3)(6^(4)) + 3root(3)(6^(4)) = 4*6^(A) First, we need to recognize that root(3)(6^(4)) is the cube root of 6 raised to the 4th power. We can combine like terms on the left side of the equation.Combine like terms: Since both terms on the left side of the equation have the same cube root, we can add them together: root(3)(6^(4)) + 3root(3)(6^(4)) = 4root(3)(6^(4))Add like terms: Now we have: 4root(3)(6^(4)) = 4*6^(A) To find the value of A, we need to equate the expressions inside the cube root to the expression on the right side of the equation. Since the coefficients (4) on both sides are the same, we can divide both sides by 4 to get rid of them. root(3)(6^(4)) = 6^(A)Equate expressions: Now we need to express the cube root of 6^4 in exponential form. The cube root of a number is the same as raising that number to the power of 1/3. Therefore, we can rewrite the left side as: (6^(4))^(1/3) = 6^(A)Express cube root: Using the property of exponents that states (a^(m))^n = a^(m*n), we can simplify the left side: 6^(4*(1/3)) = 6^(A) 6^(4/3) = 6^(A)Simplify exponents: Since the bases are the same (6), we can equate the exponents: 4/3 = A

$\sqrt[3]{6^{4}}+3 \sqrt[3]{6^{4}}=4 \cdot 6^{A}$ $\newline$ What is the value of $A$ ?

Full solution

More problems from Powers with negative bases

Related topics

643+3643=4⋅6A \sqrt[3]{6^{4}}+3 \sqrt[3]{6^{4}}=4 \cdot 6^{A} 364​+3364​=4⋅6A\newlineWhat is the value of A A A ?

$\sqrt[3]{6^{4}}+3 \sqrt[3]{6^{4}}=4 \cdot 6^{A}$ $\newline$ What is the value of $A$ ?