Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Put the quadratic into vertex form and state the coordinates of the vertex.

y=x^(2)+2x+37
Vertex Form:
y=
Vertex:
Submit Answer

Put the quadratic into vertex form and state the coordinates of the vertex. $\newline$ $y=x^{2}+2 x+37$ $\newline$ Vertex Form: $y=$ $\newline$ Vertex: $\newline$ Submit Answer

View step-by-step help

View step-by-step help

Convert equations of parabolas from general to vertex form

Full solution

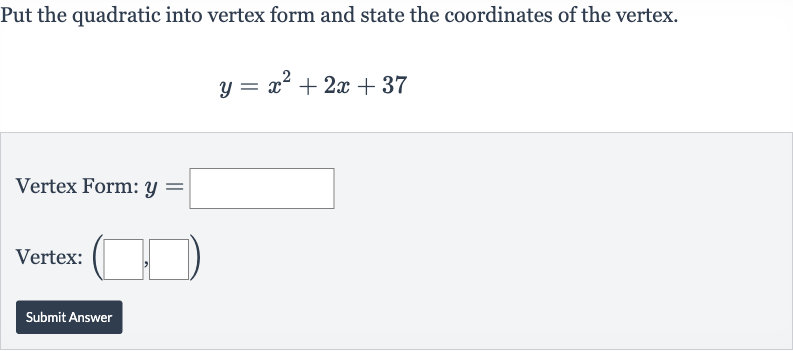
Q. Put the quadratic into vertex form and state the coordinates of the vertex.

\newline

y=x^{2}+2 x+37

\newline

Vertex Form:

y=

\newline

Vertex:

\newline

Submit Answer

Identify Vertex Form: Identify the vertex form of a parabola. The vertex form of a parabola is given by $y = a(x - h)^2 + k$ , where $(h, k)$ is the vertex of the parabola.
Complete the Square: Complete the square to rewrite the quadratic equation $y = x^2 + 2x + 37$ in vertex form. $\newline$ First, we need to focus on the $x$ -terms. We have $x^2 + 2x$ . To complete the square, we take half of the coefficient of $x$ , which is $\frac{2}{2} = 1$ , and square it, giving us $1^2 = 1$ . We will add and subtract this value inside the parentheses to maintain equality.
Rewrite Equation: Rewrite the equation by adding and subtracting the squared term. $\newline$ $y = x^2 + 2x + 1 - 1 + 37$ $\newline$ Now, group the perfect square trinomial and the constants. $\newline$ $y = (x^2 + 2x + 1) + 36$
Factor Trinomial: Factor the perfect square trinomial. $\newline$ The expression $x^2 + 2x + 1$ factors to $(x + 1)^2$ . $\newline$ So, the equation now reads $y = (x + 1)^2 + 36$ .
Write in Vertex Form: Write the equation in vertex form and identify the vertex. $\newline$ The equation in vertex form is $y = (x + 1)^2 + 36$ . $\newline$ The vertex of the parabola, given by the form $y = a(x - h)^2 + k$ , is $(h, k)$ . In our equation, $h = -1$ and $k = 36$ . $\newline$ Therefore, the vertex is $(-1, 36)$ .

More problems from Convert equations of parabolas from general to vertex form

Question

What is the focus of the parabola

y = -x^2

\newline

Simplify any fractions.

\newline

(_____ , _____)

\newline

Posted 1 month ago

Question

The equation of a parabola is

y = x^2 - 10x + 25

. Write the equation in vertex form.

\newline

Write any numbers as integers or simplified proper or improper fractions.

\newline

Posted 2 months ago

Question

In which direction does the parabola

x + y^2 = -7

\newline

\newline

\text{up}

\newline

\text{down}

\newline

\text{right}

\newline

\text{left}

Posted 2 months ago

Question

What is the vertex of the parabola

y = -4(x - 2)^2 + 2

?

\newline

(\_,\_)

Posted 2 months ago

Question

What is the axis of symmetry of the parabola

x = \frac{1}{2}(y + 3)^2 + 5

Posted 2 months ago

Question

In which direction does the parabola

x - 2y^2 = -5

\newline

\newline

\text{[A]up}

\newline

\text{[B]down}

\newline

\text{[C]right}

\newline

\text{[D]left}

Posted 2 months ago

Question

What is the vertex of the parabola

y - 8x^2 = 4

\newline

(\_,\_)

Posted 1 month ago

Question

The equation of a circle is

x^{2}+(y+4)^{2}=1

. What are the center and radius of the circle?

\newline

1

\newline

(A) The center is

(-4,0)

and the radius is

1

\newline

(B) The center is

(4,0)

and the radius is

1

\newline

(C) The center is

(0,4)

and the radius is

1

\newline

(D) The center is

(0,-4)

and the radius is

1

Posted 4 months ago

Question

y=(x-3)(x+9)

\newline

The given equation is graphed in the

x y

-plane. Which of the following are

x

-intercepts of the graph?

\newline

1

\newline

-3

-9

\newline

-3

9

\newline

3

-9

\newline

3

9

Posted 4 months ago

Question

y=2 x^{2}-5 x+7

is graphed in the

x y

-plane, which of the following characteristics of the graph is displayed as a constant or coefficient in the equation?

\newline

1

\newline

x

\newline

y

\newline

x

-coordinate of the vertex

\newline

y

-coordinate of the vertex

Posted 4 months ago