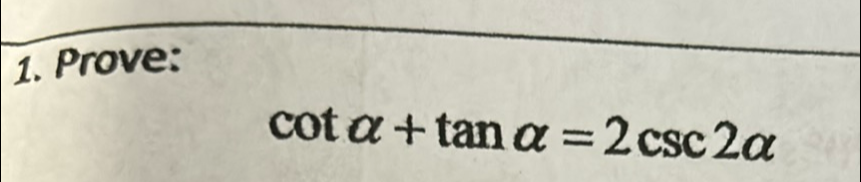AI tutor
Full solution
Q. . Prove:
- Express in terms of sine/cosine: First, let's express and in terms of sine and cosine. and .
- Add cot and tan: Now, let's add and together.
- Find common denominator: To add these fractions, we need a common denominator, which is ..
- Apply Pythagorean identity: We know that , according to the Pythagorean identity.So,
- Use double angle formula: Now, let's express the denominator in terms of the double angle formula for sine: ..
- Invert denominator: Inverting the fraction in the denominator, we get: .
- Reciprocal of sine: Finally, we know that is the reciprocal of , so . Therefore, .
More problems from Solve linear equations with variables on both sides
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help