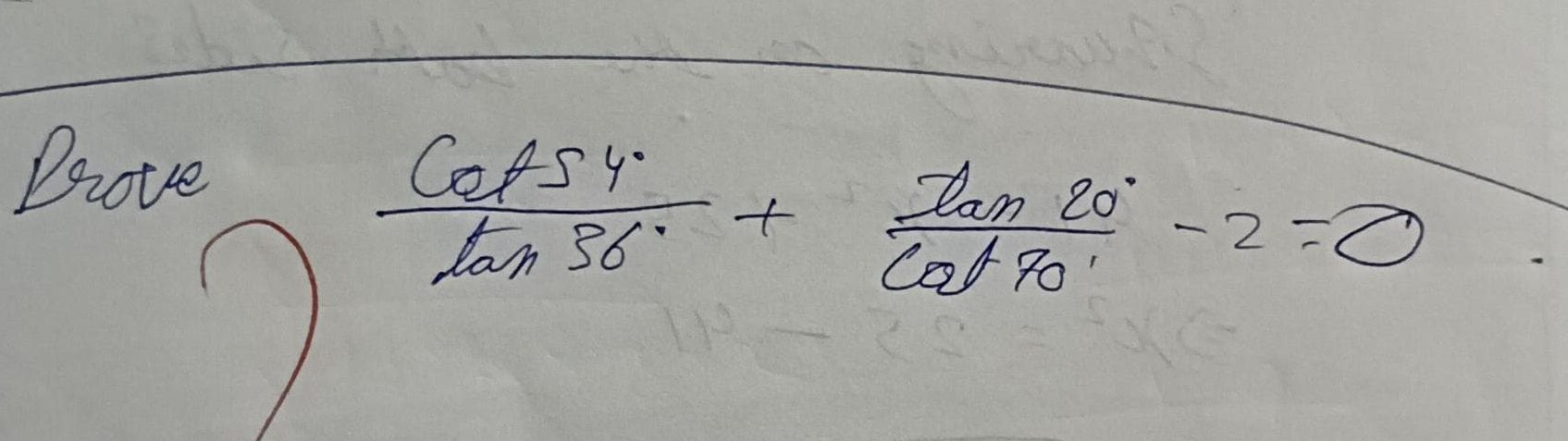AI tutor
Full solution
Q. Prove .
- Use Trigonometric Identities: We will use the fact that and that . We will also use the complementary angle identity, which states that and .
- Simplify : First, let's simplify . Since , we can rewrite as . Therefore, becomes .
- Simplify : Simplifying the expression further, we get . Since , we can rewrite as . So, the expression becomes .
- Substitute Simplified Expressions: Since , the expression simplifies to , which is just . So, simplifies to .
- Calculate Final Result: Now, let's simplify . Since , we can rewrite as . Therefore, becomes .
- Calculate Final Result: Now, let's simplify . Since , we can rewrite as . Therefore, becomes . Simplifying the expression further, we get . Since , we can rewrite as . So, the expression becomes .
- Calculate Final Result: Now, let's simplify . Since , we can rewrite as . Therefore, becomes . Simplifying the expression further, we get . Since , we can rewrite as . So, the expression becomes . Since , the expression simplifies to . So, simplifies to .
- Calculate Final Result: Now, let's simplify . Since , we can rewrite as . Therefore, becomes . Simplifying the expression further, we get . Since , we can rewrite as . So, the expression becomes . Since , the expression simplifies to . So, simplifies to . Now we have the simplified expressions: and . Substituting these into the original equation, we get .
- Calculate Final Result: Now, let's simplify . Since , we can rewrite as . Therefore, becomes . Simplifying the expression further, we get . Since , we can rewrite as . So, the expression becomes . Since , the expression simplifies to . So, simplifies to . Now we have the simplified expressions: and . Substituting these into the original equation, we get . Adding the numbers together, we have . This proves that the original expression equals .