Resources

Resources

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

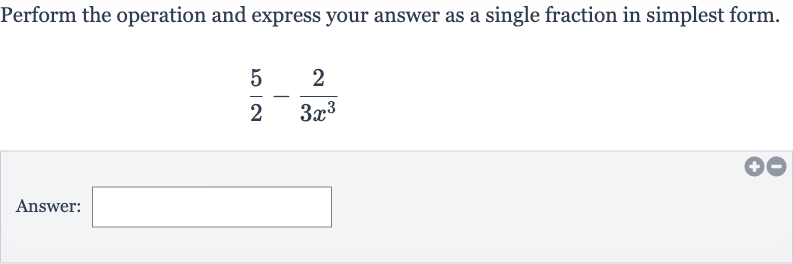
$Perform the operation and express your answer as a single fraction in simplest form. (5)/(2)-(2)/(3x^(3)) Answer:$

Perform the operation and express your answer as a single fraction in simplest form. $\newline$ $\frac{5}{2}-\frac{2}{3 x^{3}}$ $\newline$ Answer:

Full solution

Q. Perform the operation and express your answer as a single fraction in simplest form.

\newline

\frac{5}{2}-\frac{2}{3 x^{3}}

\newline

Answer:

Find Common Denominator: Find a common denominator for the two fractions. $\newline$ The common denominator for $2$ and $3x^3$ is $6x^3$ . We need to convert both fractions to have this common denominator.
Convert First Fraction: Convert the first fraction $(\frac{5}{2})$ to have the common denominator $6x^3$ . To do this, we multiply both the numerator and the denominator by $3x^3$ . $(\frac{5}{2}) \times (\frac{3x^3}{3x^3}) = (\frac{5\times 3x^3}{2\times 3x^3}) = (\frac{15x^3}{6x^3})$
Convert Second Fraction: Convert the second fraction $(\frac{2}{3x^3})$ to have the common denominator $6x^3$ . To do this, we multiply both the numerator and the denominator by $2$ . $(\frac{2}{3x^3}) \times (\frac{2}{2}) = (\frac{2\times 2}{3x^3\times 2}) = (\frac{4}{6x^3})$
Subtract Fractions: Subtract the second fraction from the first fraction. $\newline$ Now that both fractions have the same denominator, we can subtract them. $\newline$ $(\frac{15x^3}{6x^3}) - (\frac{4}{6x^3}) = \frac{15x^3 - 4}{6x^3}$
Simplify Numerator: Simplify the numerator if possible. $\newline$ In this case, the numerator $15x^3 - 4$ cannot be simplified further because the terms are not like terms.
Write Final Answer: Write the final answer. $\newline$ The simplified form of the expression is $(\frac{15x^3 - 4}{6x^3})$ .