Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

New Tab Mail - Kelvin Jones... Shopping Cart | OP... Building a Better A... What Question 6 of 10 C PREVIOUS QUESTION How many (1)/(4) inch cubes does it take to fill a box with width 3(1)/(4) inches, length 4(1)/(2) inches, and height 2(3)/(4) inches? (A) 2,574 cubes (B) 40 cubes (C) 644 cubes (D) 1,536 cubes

New Tab\newlineMail - Kelvin Jones...\newlineShopping Cart | OP...\newlineBuilding a Better A...\newlineWhat\newlineQuestion 66 of 1010\newlineC PREVIOUS QUESTION\newlineHow many \newline14\frac{1}{4} inch cubes does it take to fill a box with width \newline3143\frac{1}{4} inches, length \newline4124\frac{1}{2} inches, and height \newline2342\frac{3}{4} inches?\newline(A) 22,574574 cubes\newline(B) 4040 cubes\newline(C) 644644 cubes\newline(D) 11,536536 cubes

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find derivatives of inverse trigonometric functionsright chevron icon

Full solution

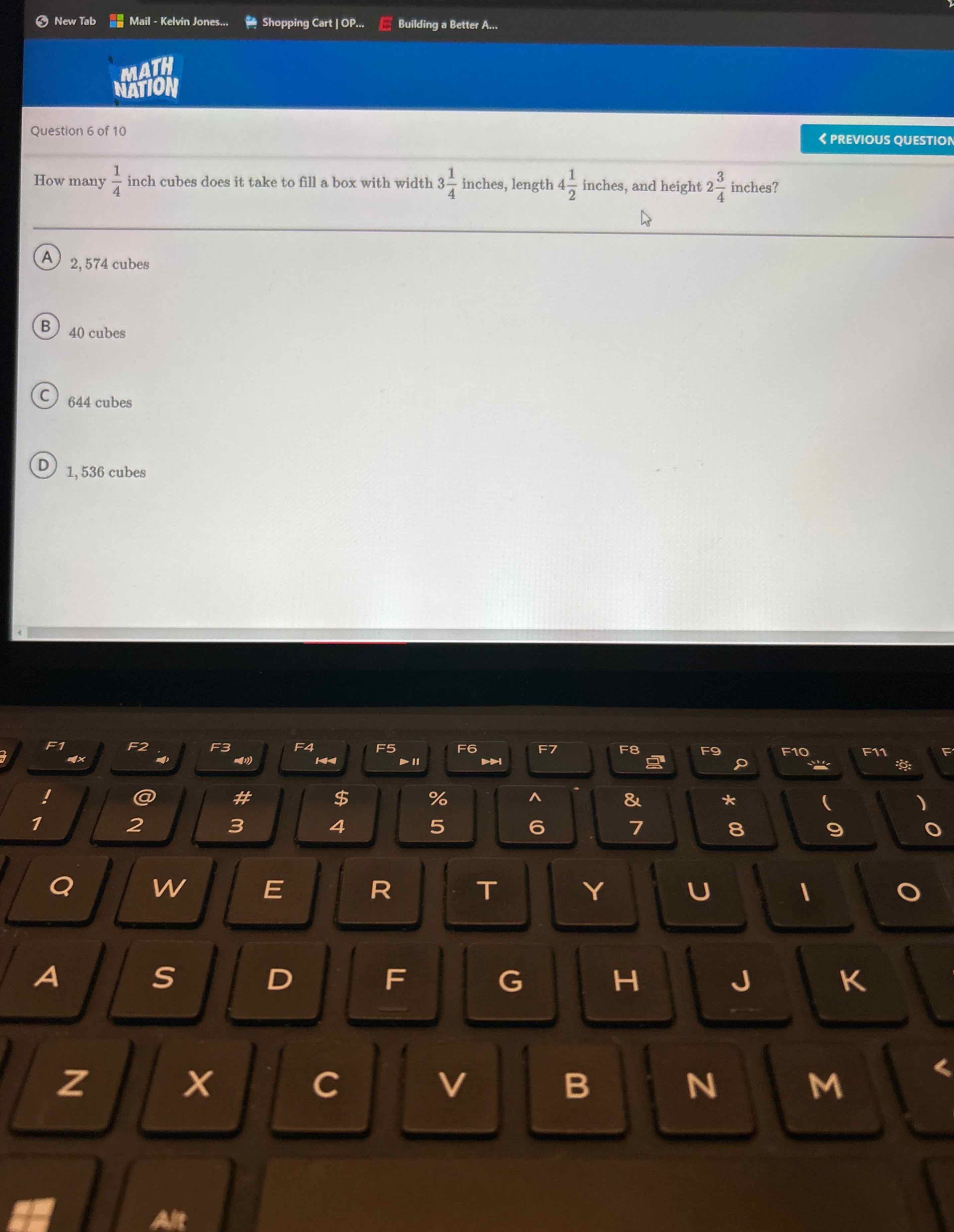
Q. New Tab\newlineMail - Kelvin Jones...\newlineShopping Cart | OP...\newlineBuilding a Better A...\newlineWhat\newlineQuestion 66 of 1010\newlineC PREVIOUS QUESTION\newlineHow many \newline14\frac{1}{4} inch cubes does it take to fill a box with width \newline3143\frac{1}{4} inches, length \newline4124\frac{1}{2} inches, and height \newline2342\frac{3}{4} inches?\newline(A) 22,574574 cubes\newline(B) 4040 cubes\newline(C) 644644 cubes\newline(D) 11,536536 cubes
  1. Convert to Improper Fractions: step_1: Convert the dimensions of the box from mixed fractions to improper fractions. Width = 3143 \frac{1}{4} inches = 134\frac{13}{4} inches, Length = 4124 \frac{1}{2} inches = 92\frac{9}{2} inches, Height = 2342 \frac{3}{4} inches = 114\frac{11}{4} inches.
  2. Calculate Volume: step_2: Calculate the volume of the box using the formula Volume=Width×Length×HeightVolume = Width \times Length \times Height. Volume=(134)×(92)×(114)Volume = \left(\frac{13}{4}\right) \times \left(\frac{9}{2}\right) \times \left(\frac{11}{4}\right) inches3^3.
  3. Perform Multiplication: step_3: Perform the multiplication to find the volume. Volume = (13×9×11)/(4×2×4)=1287/32=40.21875(13 \times 9 \times 11) / (4 \times 2 \times 4) = 1287 / 32 = 40.21875 cubic inches.
  4. Calculate Cube Volume: step_4: Calculate the volume of one 14\frac{1}{4} inch cube. Volume of one cube = (14)×(14)×(14)=164\left(\frac{1}{4}\right) \times \left(\frac{1}{4}\right) \times \left(\frac{1}{4}\right) = \frac{1}{64} cubic inches.
  5. Determine Cube Fit: step_5: Determine how many 14\frac{1}{4} inch cubes fit into the box. Number of cubes = Total volume of box / Volume of one cube = 40.21875(164)=2574\frac{40.21875}{\left(\frac{1}{64}\right)} = 2574 cubes.

More problems from Find derivatives of inverse trigonometric functions

Question
Find lim⁡θ→π2tan⁡2(θ)[1−sin⁡(θ)] \lim_{\theta \rightarrow \frac{\pi}{2}} \tan ^{2}(\theta)[1-\sin (\theta)] .\newlineChoose 11 answer:\newline(A) 00\newline(B) 12 \frac{1}{2} \newline(C) −2-2\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 3 months ago

Question
Find lim⁡θ→π2sin⁡2(2θ)1−sin⁡2(θ) \lim _{\theta \rightarrow \frac{\pi}{2}} \frac{\sin ^{2}(2 \theta)}{1-\sin ^{2}(\theta)} \newlineChoose 11 answer:\newline(A) 11\newline(B) 22\newline(C) 44\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 3 months ago

Question
Find lim⁡x→3x−34x+4−4 \lim _{x \rightarrow 3} \frac{x-3}{\sqrt{4 x+4}-4} .\newlineChoose 11 answer:\newline(A) −4-4\newline(B) 11\newline(C) 22\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 3 months ago

Question
Find lim⁡x→−47x+28x2+x−12 \lim _{x \rightarrow-4} \frac{7 x+28}{x^{2}+x-12} .\newlineChoose 11 answer:\newline(A) 11\newline(B) 77\newline(C) −1-1\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 3 months ago

Question
Find lim⁡x→−3x+34−2x+22 \lim _{x \rightarrow-3} \frac{x+3}{4-\sqrt{2 x+22}} .\newlineChoose 11 answer:\newline(A) −3-3\newline(B) −4-4\newline(C) −34 -\frac{3}{4} \newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 3 months ago

Question
Find lim⁡x→15x+4−3x−1 \lim _{x \rightarrow 1} \frac{\sqrt{5 x+4}-3}{x-1} .\newlineChoose 11 answer:\newline(A) 35 \frac{3}{5} \newline(B) 56 \frac{5}{6} \newline(C) 11\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 3 months ago

Question
Find lim⁡x→−2x3+3x2+2xx+2 \lim _{x \rightarrow-2} \frac{x^{3}+3 x^{2}+2 x}{x+2} .\newlineChoose 11 answer:\newline(A) 66\newline(B) 00\newline(C) 22\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 3 months ago

Question
Find lim⁡x→π2cot⁡2(x)1−sin⁡(x) \lim _{x \rightarrow \frac{\pi}{2}} \frac{\cot ^{2}(x)}{1-\sin (x)} \newlineChoose 11 answer:\newline(A) −1-1\newline(B) −π2 -\frac{\pi}{2} \newline(C) 22\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 3 months ago

Question
Find lim⁡x→π2sin⁡(2x)cos⁡(x) \lim _{x \rightarrow \frac{\pi}{2}} \frac{\sin (2 x)}{\cos (x)} .\newlineChoose 11 answer:\newline(A) 12 \frac{1}{2} \newline(B) 11\newline(C) 22\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 3 months ago

Question
Find lim⁡θ→π4cos⁡(2θ)2cos⁡(θ)−1 \lim _{\theta \rightarrow \frac{\pi}{4}} \frac{\cos (2 \theta)}{\sqrt{2} \cos (\theta)-1} .\newlineChoose 11 answer:\newline(A) 22\newline(B) 12 \frac{1}{2} \newline(C) 2 \sqrt{2} \newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 3 months ago

View all (16)