AI tutor
Full solution
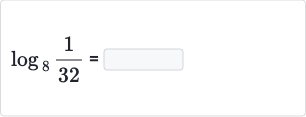
Q.
- Recognize logarithm of : We are asked to find the value of the logarithm of with base . The first step is to recognize that the logarithm of to any base is , because any number to the power of is .
- Express as a power of : Now we need to consider the part. We can express as a power of to use the quotient property of logarithms, which states that the logarithm of a quotient is the difference of the logarithms. can be written as , and since is , we can rewrite as .
- Simplify the expression: Using the property of exponents , we can simplify to , which simplifies to , confirming our previous statement that is .
- Write as difference of logarithms: Now we can write the original expression as the difference of two logarithms:Since we already know , we only need to evaluate .
- Express as a power of : We can express as to the power of some number. Since is and is , we can find the exponent by solving for in .
- Solve for the exponent: Solving the equation gives us . Therefore, is to the power of , and we can write:
- Apply power property of logarithms: Using the power property of logarithms, which states that , we get:
- Evaluate : Since the logarithm of a number to the same base is , . Therefore:
- Combine results to find the value: Now we can combine our results to find the value of the original expression:
More problems from Evaluate logarithms using properties
QuestionGet tutor help
QuestionGet tutor help