Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

log_(5)625=

$\log _{5} 625=$

View step-by-step help

View step-by-step help

Convert between exponential and logarithmic form: all bases

Full solution

Q.

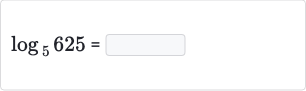
\log _{5} 625=

Identify base, number, and unknown exponent: Identify the base ( $b$ ), the number ( $x$ ), and the unknown exponent ( $y$ ) in the logarithmic equation $\log_{5}625 = y$ . $\newline$ Here, $b = 5$ and $x = 625$ . We need to find the value of $y$ such that $5^y = 625$ .
Recall logarithm and exponential form: Recall that the logarithm $\log_{b}x = y$ is equivalent to the exponential form $b^{y} = x$ . We need to find the power $y$ to which the base $5$ must be raised to get $625$ .
Determine if $625$ is a power of $5$ : Determine if $625$ is a power of $5$ . We know that $5^2 = 25$ and $5^4 = 625$ . $\newline$ Therefore, $5$ raised to the power of $4$ equals $625$ .
Write exponential equation using base $5$ and exponent $4$ : Write the exponential equation using the base $5$ and the exponent $4$ to equal $625$ . $\newline$ The equation is $5$ ^ $4$ = $625$ .
Value of y in logarithmic equation: Since $5^4 = 625$ , the logarithmic equation $\log_{5}625$ equals $4$ . $\newline$ This means that the value of $y$ in the equation $\log_{5}625 = y$ is $4$ .

More problems from Convert between exponential and logarithmic form: all bases

Question

\newline

\frac{5}{6} \div \frac{9}{4}=

Posted 3 months ago

Question

\newline

\frac{8}{3} \div \frac{5}{3}=

Posted 3 months ago

Question

\newline

\frac{5}{4} \div \frac{3}{5}=

Posted 3 months ago

Question

\newline

\frac{3}{4} \div \frac{3}{4}=

Posted 3 months ago

Question

Write the expression in exponential form.

\newline

6 \times 6 \times 6 \times 6 \times 6=

Posted 3 months ago

Question

Write the expression in exponential form.

\newline

9 \times 9 \times 9 \times 9 \times 9 \times 9 \times 9=

Posted 3 months ago

Question

The value of Vishal's car is depreciating exponentially.

\newline

The relationship between

V

, the value of his car, in dollars, and

t

, the elapsed time, in years, since he purchased the car is modeled by the following equation.

\newline

V=22,500 \cdot 10^{-\frac{t}{12}}

\newline

How many years after purchase will Vishal's car be worth

\$ 10,000

\newline

Give an exact answer expressed as a base

-10

\newline

Posted 3 months ago

Question

A scientist measures the initial amount of Carbon

-14

in a substance to be

25

\newline

The relationship between

A

, the amount of Carbon

-14

remaining in that substance, in grams, and

t

, the elapsed time, in years, since the initial measurement is modeled by the following equation.

\newline

A=25 e^{-0.00012 t}

\newline

In how many years will the substance contain exactly

20

(\mathrm{g})

-14

\newline

Give an exact answer expressed as a natural logarithm.

\newline

Posted 3 months ago

Question

Which of the following is equivalent to

\log _{7}(a) \cdot \log _{b}(7)

\newline

1

\newline

\log (7)

\newline

\log (7 a)

\newline

\log _{a}(b)

\newline

\log _{b}(a)

Posted 3 months ago

Question

Which of the following is equivalent to

\log (a) \cdot \log _{a}(5)

\newline

1

\newline

\log (a)

\newline

\log (5)

\newline

\log (5 a)

\newline

\log _{a}(5 a)

Posted 3 months ago