Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

log_(4)(1)/(2)=

$\log _{4} \frac{1}{2}=$

View step-by-step help

View step-by-step help

Evaluate logarithms using properties

Full solution

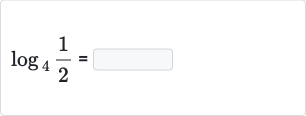
Q.

\log _{4} \frac{1}{2}=

Evaluate logarithm of $\frac{1}{2}$ : We need to evaluate the logarithm of $\frac{1}{2}$ with base $4$ . The logarithm of a number is the exponent to which the base must be raised to produce that number.
Express $\frac{1}{2}$ as a power of $4$ : First, let's express $\frac{1}{2}$ as a power of $4$ . Since $4$ is $2^2$ , we can write $\frac{1}{2}$ as $2^{-1}$ . This is because $\frac{1}{2}$ is the reciprocal of $2$ , and the reciprocal of a number is equal to that number raised to the power of $4$ $0$ .
Rewrite logarithm using power of $4$ : Now, we can rewrite the logarithm using the power of $4$ . Since $2$ is the square root of $4$ , we can express $2$ as $4^{1/2}$ . Therefore, $2^{-1}$ can be written as $(4^{1/2})^{-1}$ .
Simplify using properties of exponents: Using the properties of exponents, $(4^{\frac{1}{2}})^{-1}$ simplifies to $4^{-\frac{1}{2}}$ . This is because when you raise a power to a power, you multiply the exponents.
Rewrite logarithm as log base $4$ : Now we can rewrite the original logarithm as $\log_{4}(4^{-\frac{1}{2}})$ .
Simplify using property of logarithms: Using the property of logarithms that $\log_b(b^x) = x$ , we can simplify $\log_{4}(4^{-\frac{1}{2}})$ to just $-\frac{1}{2}$ .
Simplify using property of logarithms: Using the property of logarithms that $\log_b(b^x) = x$ , we can simplify $\log_{4}(4^{-\frac{1}{2}})$ to just $-\frac{1}{2}$ .Therefore, the value of $\log_{4}(\frac{1}{2})$ is $-\frac{1}{2}$ .

More problems from Evaluate logarithms using properties

Question

\newline

\frac{5}{6} \div \frac{9}{4}=

Posted 3 months ago

Question

\newline

\frac{8}{3} \div \frac{5}{3}=

Posted 3 months ago

Question

\newline

\frac{5}{4} \div \frac{3}{5}=

Posted 3 months ago

Question

\newline

\frac{3}{4} \div \frac{3}{4}=

Posted 3 months ago

Question

Write the expression in exponential form.

\newline

6 \times 6 \times 6 \times 6 \times 6=

Posted 3 months ago

Question

Write the expression in exponential form.

\newline

9 \times 9 \times 9 \times 9 \times 9 \times 9 \times 9=

Posted 3 months ago

Question

The value of Vishal's car is depreciating exponentially.

\newline

The relationship between

V

, the value of his car, in dollars, and

t

, the elapsed time, in years, since he purchased the car is modeled by the following equation.

\newline

V=22,500 \cdot 10^{-\frac{t}{12}}

\newline

How many years after purchase will Vishal's car be worth

\$ 10,000

\newline

Give an exact answer expressed as a base

-10

\newline

Posted 3 months ago

Question

A scientist measures the initial amount of Carbon

-14

in a substance to be

25

\newline

The relationship between

A

, the amount of Carbon

-14

remaining in that substance, in grams, and

t

, the elapsed time, in years, since the initial measurement is modeled by the following equation.

\newline

A=25 e^{-0.00012 t}

\newline

In how many years will the substance contain exactly

20

(\mathrm{g})

-14

\newline

Give an exact answer expressed as a natural logarithm.

\newline

Posted 3 months ago

Question

Which of the following is equivalent to

\log _{7}(a) \cdot \log _{b}(7)

\newline

1

\newline

\log (7)

\newline

\log (7 a)

\newline

\log _{a}(b)

\newline

\log _{b}(a)

Posted 3 months ago

Question

Which of the following is equivalent to

\log (a) \cdot \log _{a}(5)

\newline

1

\newline

\log (a)

\newline

\log (5)

\newline

\log (5 a)

\newline

\log _{a}(5 a)

Posted 3 months ago